Rotational dynamics#

Much like how the translational dynamics inherently makes use of the concepts of linear momentum and forces, the rotational dynamics can be studied by making use of angular momentum (moment of linear momentum) and moments of forces.

In this next section, e will derive the relevant equations by making use of the system of particles from before (also shown in figure below). We also introduce a point \(O\) as we know that the concept of a moment of a vector is defined relative to some point in space.

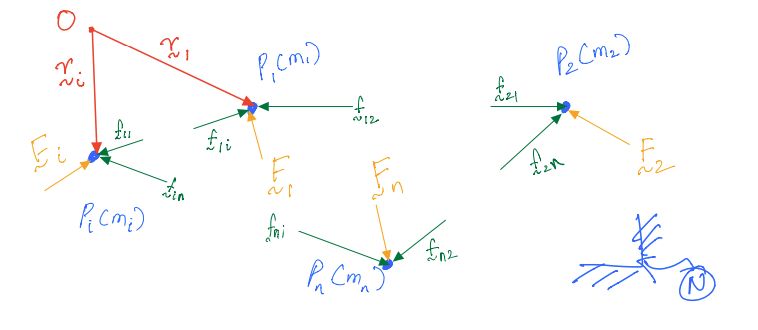
../_images/earth-sat-13.png

We now begin by considering the equation of translational motion for \(P_1\):

\[{\mathbf{{F}}_1} + \sum_{k=1}^n {\mathbf{{f}}_{1k}} = {m_1}{{}^{N}{\mathbf{{a}}}^{p_1}} \tag{11.3}\]

We can cross multiply it on both the right and left sides by \({r}_1\), the position vector from \(O\) to \(P_1\):

\[{{r}_1} \times ({\mathbf{{F}}_1} + \sum_{k=1}^n {\mathbf{{f}}_{1k}}) = {{r}_1} \times {m_1}{{}^{N}{\mathbf{{a}}}^{p_1}} \tag{11.8}\]

In essence, what we have done is taken the moment about point \(O\) of vectors on the right and left hand sides.

We can repeat this process for the other particles \(P_2\), \(P_i\), and \(P_n\). In other words, we can take the moment about point \(O\) for each particle’s translational equations, as given by equations \(11.4\), \(11.5\), and \(11.6\).

For \(\mathbf{P_2}\)

\[{{r}_2} \times {\mathbf{{F}}_2} + \sum_{k=1}^n {\mathbf{{f}}_{2k}} = {{r}_2} {m_2}{{}^{N}{\mathbf{{a}}}^{p_2}} \tag{11.9}\]

For \(\mathbf{P_i}\)

\[{{r}_i}{\mathbf{{F}}_i} + \sum_{k=1}^n {\mathbf{{f}}_{ik}} = {{r}_i}{m_i}{{}^{N}{\mathbf{{a}}}^{p_i}} \tag{11.10}\]

For \(\mathbf{P_n}\)

\[{{r}_n}{\mathbf{{F}}_n} + \sum_{k=1}^n {\mathbf{{f}}_{nk}} = {{r}_n}{m_n}{{}^{N}{\mathbf{{a}}}^{p_n}}\tag{11.11}\]

We can now add up equations \(11.8\) and \(11.11\) to get:

\[\sum_{j=1}^n {\mathbf{{r}}_{j}} \times {\mathbf{{F}}_{j}} + \sum_{j=1}^n \sum_{k=1}^n {\mathbf{{r}}_{j}} \times {\mathbf{{f}}_{jk}} = \sum_{j=1}^n {\mathbf{{r}}_{j}} \times ({m_j}{{}^{N}\mathbf{{a}}^{p_j}}) \tag{11.12}\]

Let’s examine each term of equation \(11.12\):

The first term, \(\sum_{j=1}^n {\mathbf{{r}}_{j}} \times {\mathbf{{F}}_{j}}\), is the sum of moments of the external forces about the point \(O\).

The second term, \(\sum_{j=1}^n \sum_{k=1}^n {\mathbf{{r}}_{j}} \times {\mathbf{{f}}_{jk}}\), can be proven to be zero. Take time to do this independently to help with your understanding.

The third term, \(\sum_{j=1}^n {\mathbf{{r}}_{j}} \times ({m_j}{{}^{N}\mathbf{{a}}^{p_j}})\), is a more complex term. Examination starts by looking at the defination of angular of a syetm of particles, given below:

\[{}^{N}{\mathbf{{H}}}^{S/O} = \sum_{j=1}^n {{\mathbf{{r}}}_j} \times {m_j}{{}^{N}\mathbf{{v}}^{p_j}}\]

So, the time derivative of this system’s angular momentum vector taken from the inertial frame \(N\) is given as:

\[ \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/O} = \left(\sum_{j=1}^n \frac{{}^N d} {\mathrm{d}t} {{\mathbf{{r}}}_j} \times {m_j}{{}^{N}\mathbf{{v}}^{p_j}}\right) + \left(\sum_{j=1}^n {}^{N}{{\mathbf{{r}}}_j} \times {m_j}{{}^{N}\mathbf{{a}}^{p_j}}\right) \]
\[\left(\sum_{j=1}^n {}^{N}{{\mathbf{{r}}}_j} \times {m_j}{{}^{N}\mathbf{{a}}^{p_j}}\right) = \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/O} + \left(\sum_{j=1}^n {{\mathbf{{r}}}_j} \times {m_j}{{}^{N}\mathbf{{a}}^{p_j}}\right) \tag{11.13}\]

So, \(11.12\) becomes:

\[\sum {\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/O} = {\frac d {\mathrm{d}t}} {}^{N}{\mathbf{{H}}}^{S/O} + \left(\sum_{j=1}^n {{\mathbf{{r}}}_j} \times {m_j}{{}^{N}\mathbf{{a}}^{p_j}}\right) \tag{11.13}\]

Where \(\sum {\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/O}\) is the sum of moments of the external forces about the point \(O\).

By introdcuing a point, \(Q\), fixed in inertial frame \(N\) and defining two new position vectors as shown below, we can further synthesise the expression \({{}^{N}\mathbf{{a}}^{p_j}}\) in terms of mass centres.

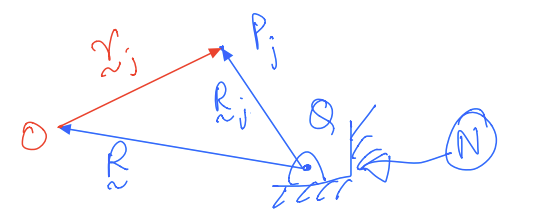
../_images/earth-sat-20_cut.png

Hence we can see:

\[{\mathbf{{r}}}_j = {\mathbf{{R}}}_j - {\mathbf{{r}}}\]

and

\[{\frac d {\mathrm{d}t}} {\mathbf{{r}}}_j = {}^{N}{\mathbf{{v}}}^{p_j} - {}^{N}{\mathbf{{v}}}^{O}\]

So, \(11.13\) can now be rewritten finally in a much simpler form as:

\[\sum{\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/{O}} = \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/O} - \left(\sum_{j=1}^n m_j {}^{N}{\mathbf{{v}}}^{p_j}\right) \times {}^{N}{\mathbf{{v}}}^{O}\]

Or…

\[\sum{\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/{O}} = {}^{N}{\frac d {\mathrm{d}t}} {}^{N}{\mathbf{{H}}}^{S/O} - \left(m {}^{N}{\mathbf{{v}}}^{S^*}\right) \times {}^{N}{\mathbf{{v}}}^{O}\]

It is important to note two special cases:

  1. \(O\) is fixed in \(N\):

\[\sum{\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/{O}} = \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/O}\]

  1. \(O\) is the mass centre \(S^*\):

\[\sum{\mathbf{{M}}}^{{{{\mathbf{{F}}}_i}/{S^*}}} = \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/{S^*}}\]

Kinetics Summary The topics covered up until this point are briefly summarised in this section as a refresher to help with understanding.

We began by examining the equations of motion of a single particle \(P\) by Newton’s second law:

\[ \mathbf{{F}} = m^N\mathbf{{a}}^p \]

Then, we looked at a system of two particles and used that as a stepping stone towards deriving a generalised Newton’s second law for a system of any number of particles. This resulted in:

\[ \mathbf{{F}} = m{}^N\mathbf{{a}}^{S^*} \]

Where:

  • \(\mathbf{{F}}\) is the resultant force on the system,

  • \(m\) is the total mass,

  • \({}^N\mathbf{{a}}^{S^*}\) is the acceleration of the mass centre.

We then used the generalized Newton’s second law to derive the rotational dynamics of the system relative to a frame \(N\) by taking the moment of the translational motion about some arbitrary point \(O\). The equations for rotational motion were then found to be:

\[\sum{\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/{O}} = \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/O} - \left(m {}^{N}{\mathbf{{v}}}^{S^*}\right) \times {}^{N}{\mathbf{{v}}}^{O}\]

Where:

  • \(\sum{\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/{O}}\) is the sum of moments from external forces,

  • \(\frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{S/O}\) is the rate of change of \({\mathbf{{H}}}\) of \(S\) about \(O\). As this rotational equation was derived from the generalized Newton’s law, this result is also general. By that, we mean that this applies to general 3D rotational motion of a system of particles, \(S\), relative to an inertial frame, \(N\). Therefore, it can be easily used to study more specific types of planar motion (e.g., rotation about a fixed axis and general plane motion) by starting from this general set of equations and applying appropriate analysis to the given problem.

Lastly, we saw that the above equation simplifies when the point \(O\) is either:

  • case 1: a point that is fixed in an inertial frame; and/or

  • case 2: the mass centre.

In both cases, the last term involving cross products on the right-end side of the rotational equation drop out.