JN3: Practice Activity 2#
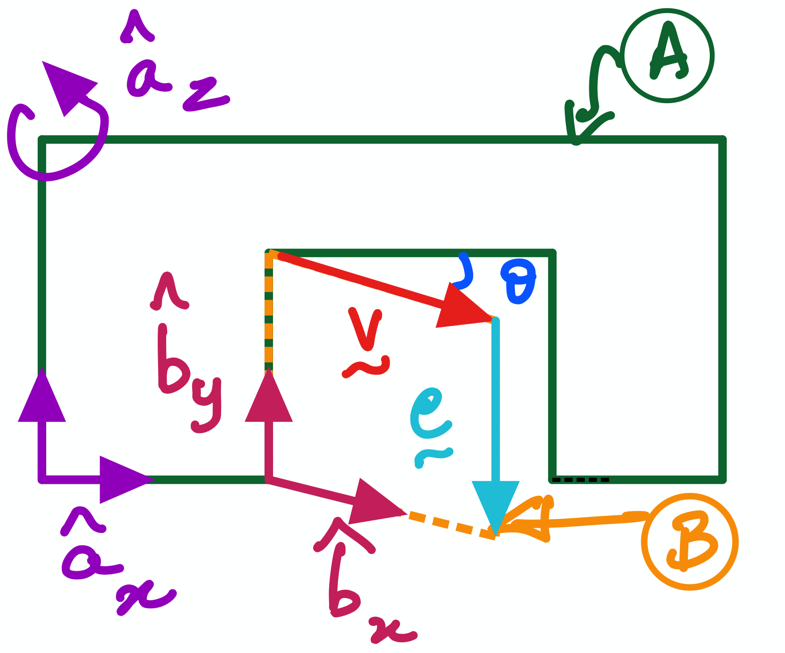
Fig. 6 Motion of a door \(B\) relative to wall \(A\).#
This notebook continues to build your dynamics knowledge using the door-wall example (see figure above), that was used in Practice Activity 1(PA1). This is an interactive notebook that is a companion to the in-class lectures; specifically this notebook addresses the Practice Activity 2.
The code in Sections 2 and 3 of this notebook are repeated from PA1. Section 4 is adapted from PA1; the modifications in this notebook are to the variable names for the vectors \(\bf v\) and \(\bf e\). The remaining content specifically addresses PA2.
Create scalars using “symbols”#
from sympy import symbols
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 1
----> 1 from sympy import symbols
ModuleNotFoundError: No module named 'sympy'
v, theta, e = symbols('v theta e')
v
theta
e
Creating Reference Frames#
A and B are reference frames. Let’s create them using SymPy!
from sympy.physics.mechanics import ReferenceFrame
A = ReferenceFrame('A')
B = ReferenceFrame('B')
Create the vectors in B-frame (slightly modified from PA1)#
In this section, we use the variable names v_vec_B and e_vec_B for \(\bf v\) and \(\bf e\) expressed in the unit vectors of the B referenece frame.
v_vec_B = v*B.x
v_vec_B
e_vec_B = -e*B.y
e_vec_B
PA2: Use the trignometric functions sine and cosine to rewrite the vectors in the A-frame#
We first import the trignometric functions for sine and cosine from sympy; these are written in their short forms as cos and sin. The importing from sympy is done in the following line:
from sympy import sin, cos
Then, we define the vector \(\bf v\) as expressed in the unit vectors attached to the frame A using the variable name v_vec_A in the following manner:
v_vec_A = v * (cos(theta)*A.x + sin(theta)*A.z)
v_vec_A
Exercsie: Can you write the same for the vector e?#
Can you define the vector \(\bf e\) expressed in the unit vectors attached to the frame A? You should use a variable name e_vec_A to do so in the cell below:


