Vector Calculus

The area of calculus we are concerned with is the time derivatives of vectors which result in velocities and accelerations.

In the case of vector, it is critical to consider the reference frame when computing derivatives. This is not the case for scalars.

Caution

Computing the time derivative from frame \(A\) of any arbitrary vector \(\vec{x}\), we must express the vector in unit vectors attached.

If the component form of \(\vec{x}\) is given in the frame \(A\) by:

(22)\[{\bf x} = x_1\hat{\bf a}_x + x_2\hat{\bf a}_y + x_3\hat{\bf a}_z\]

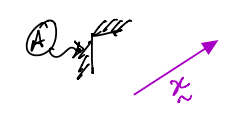
then

(23)\[\frac{{}^{A}d{\bf x}}{d\theta} \triangleq \left(\frac{d{x_1}}{d\theta}\right)\hat{\bf a}_x + \left(\frac{d{x_2}}{d\theta}\right)\hat{\bf a}_y + \left(\frac{d{x_3}}{d\theta}\right)\hat{\bf a}_z\]

Door-wall example

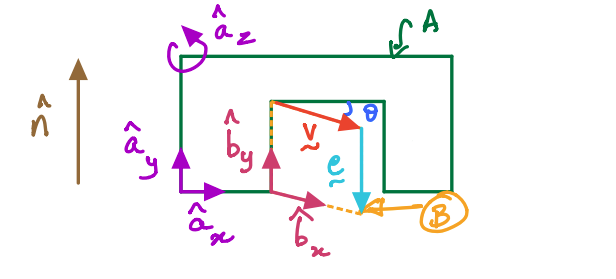
Notation:

\(\frac{{}^{A}d{\bf e}}{dt}\) is the time derivative of the vector \({\bf e}\) when observed from the reference frame A. So, \({\bf e}= -h\hat{\bf b}_y = -h\hat{\bf a}_y\).

Therefore,

(24)\[\frac{{}^{A}d{\bf e}}{dt} = \frac{{}^{A}d(-h\hat{\bf a}_y)}{dt} = 0 \text{ (zero vector)}\]

So, how can we compute the derivative of a vector using SymPy?

Another example:

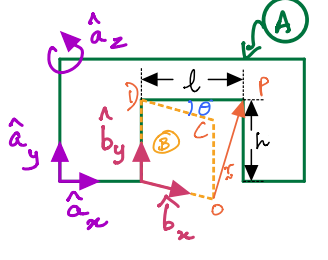
\(O\), \(C\), \(D\) and \(P\) are points as shown in the figure. \(l\) and \(h\) are the length and height of the door. \(\theta\) is time-varying. You are asked to find (i.e., compute symbolic expressions) for the following:

\[\frac{{}^{A}d{\bf r}}{dt}\]

and

\[\frac{{}^{B}d{\bf r}}{dt}.\]

Additionally, you are instructed that all final answers must be expressed in unit vectors attached to the \(A\)-frame.

Solution

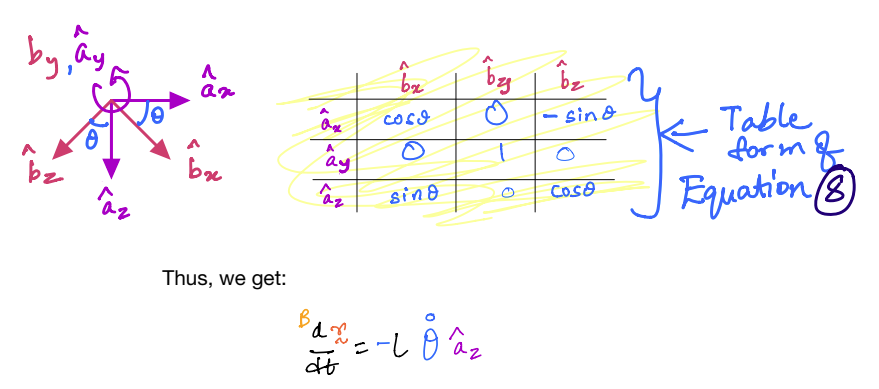
The above example demonstrated the difference between taking time derivatives of the same vector from two frames.

Properties of Vector Derivatives

The following four properties are useful in computing derivatives of vectors.

Property 1: If \(\bf a\) and \(\bf b\) are two vectors expressed in a reference frame \(D\), then the time derivative of their vector sum, taken from the frame \(D\) is:

\[\frac{{}^{D}d{}}{dt} ({\bf a} + {\bf b}) = \frac{{}^{D}d{\bf a}}{dt} + \frac{{}^{D}d{\bf b}}{dt}\]

Property 2: If \(\bf a\) is a vector expressed in a reference frame \(C\) and \(\lambda\) is some arbitrary scalar (not necessarily a constant), then the time derivative of their product is:

\[\frac{{}^{C}d{ (\lambda {\bf a})}}{dt} = \frac{d{\lambda}}{dt} {\bf a} + \lambda \frac{{}^{C}d{\bf a}}{dt}\]

Property 3: If \(\bf a\) and \(\bf b\) are two vectors expressed in a reference frame \(E\), then the derivative of their dot product with respect to some scalar parameter \(\alpha\) is:

\[\frac{d{}}{d \alpha} ({\bf a} \cdot {\bf b}) = \frac{{}^{E}d{\bf a}}{d\alpha} \cdot {\bf b} + {\bf a} \cdot \frac{{}^{E}d{\bf b}}{d\alpha}\]

Property 4: If \(\bf a\) and \(\bf b\) are two vectors expressed in some reference frame \(A\), then the derivative of their cross product taken with respect to some scalar parameter \(\gamma\) from the frame \(A\) is:

\[\frac{{}^{A}d{}}{d \gamma} ({\bf a} \times {\bf b}) = \frac{{}^{A}d{\bf a}}{d\gamma} \times {\bf b} + {\bf a} \times \frac{{}^{A}d{\bf b}}{d\gamma}\]