The Axisymmetric, Variable Mass Cylinder

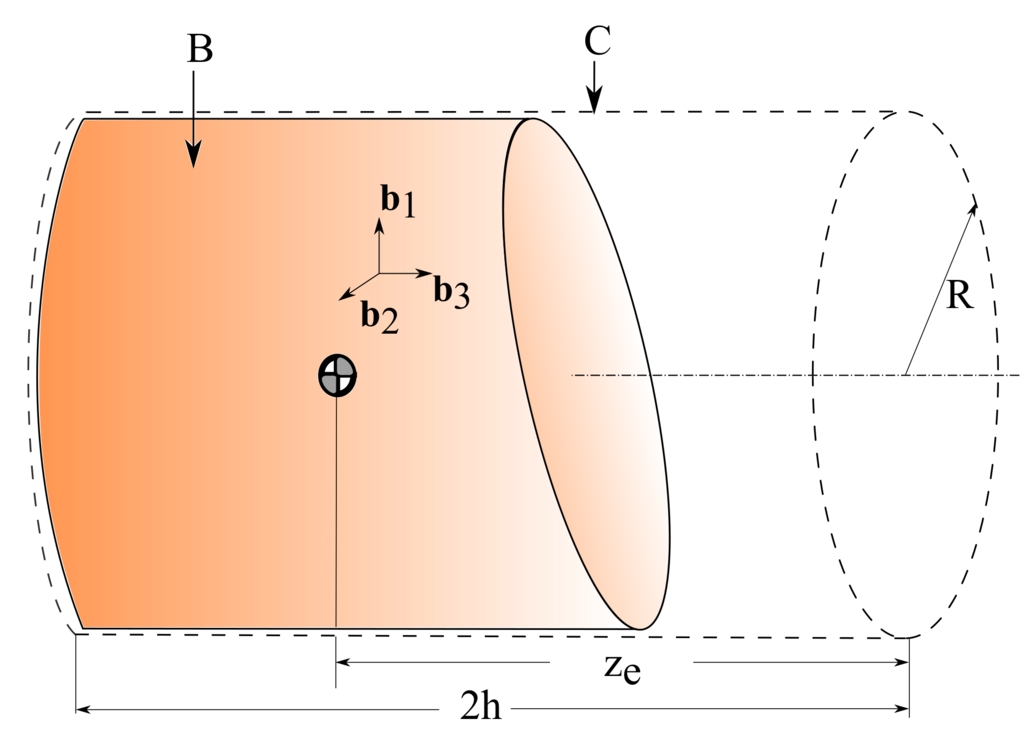
Fig. 3 Variable mass cylinder.

Figure Fig. 3 is that of a system that is initially a cylinder as represented by the dashed lines. The mass and inertia of this system is allowed to vary with time. As in the case of rockets, combustion is one plausible cause for these time-varying properties. Thus, at a general instant, some parts of the system may be solid while other parts are fluid. The solid part of the system is denoted \(B\). The dotted line represents a control region \(C\) of constant volume and surface area that has the same shape as the original cylinder and is rigidly attached to \(B\). Only matter within \(C\) at any instant is considered to make up the system. Interest here is in visualizing the motion of variable mass cylinders and understanding their nutational stability.

Equations (11)-(13) govern the attitude motion of the variable mass cylinder while Equations (17), (29), and (30) are the solutions to the angular speeds. Eke and Wang [Eke and Wang, 1995] identified idealized burn scenarios of which three are examined here. They are named the uniform burn, end burn, and radial burn. Each of these burns is explained in their respective sections. Inertia change due to fluid mass is neglected in all burn cases. The assumed properties of the system in creating the results presented are as follows. For the presented results, the density of the rigid propellant is assumed to be \(1000\) kg/m\(^3\). The initial angular speeds are assumed to be \(\omega_0=0.2\) rad/s, and \(\omega_{30} = 0.3\) rad/s; note that in a realistic rocket scenario, the spin rate would be an order of magnitude greater than the transverse rates. The duration of the burn is assumed to be \(100\) s unless mentioned otherwise. Other assumptions concerning the geometry are discussed under each burn scenario.