Uniform Burn#
Theory#
A uniformly burning cylinder is one in which the mass of the system varies as a function of time while the dimensions of the unburned portion of the cylinder are the same as that of the original cylinder; radius and length of the cylinder are both assumed to be \(1\)m. Thus, its instantaneous central moment of inertia scalars are
and
This is an example of a variable mass system where the radii of gyration are constant where \(k_1^2 = \frac{R^2}{4} + \frac{h^2}{3}\) and \(k_3^2 = \frac{R^2}{4}\). The time derivatives of the moment of inertia are
The resulting spin and transverse rates are obtained from Equations (17) and (28) as
where \(\Gamma(t) \triangleq \left(\frac{m}{m_0}\right)^{\frac{2h^2}{3k_1^2}}\). Prior to the start of the burn \(m = m_0\) so \(\Gamma = 1\). As the burn proceeds \(\Gamma\) decreases with time but is always non-negative. Thus, the transverse angular rate also decreases with time for a uniformly burning cylinder. Then Equation (39) gives the nutation angle for this system
where \(K = \frac{k_1^2 \omega_0}{k_3^2 \omega_{30}}\). Since \(K\) is constant and \(\Gamma(t)\) is decreasing with time, the nutation angle is also a decreasing parameter with time. This reduction in the transverse oscillations of a variable mass system by the exhaust gas is referred to as jet damping of a rocket.
The rotation of \(\boldsymbol{\omega}\) about \({\bf b}_3\) and \({\bf n}_h\) was discussed in the earlier section on generic axisymmetric variable mass systems. Figure Fig. 4 visualizes the first of these rotations for the uniformly burning cylinder, assuming \(k_3 > k_1\). The angular velocity vector traces a spiral in the transverse plane as it rotates about the symmetry axis \({\bf b}_3\) in a counter-clockwise direction and eventually converges to the symmetry axis.
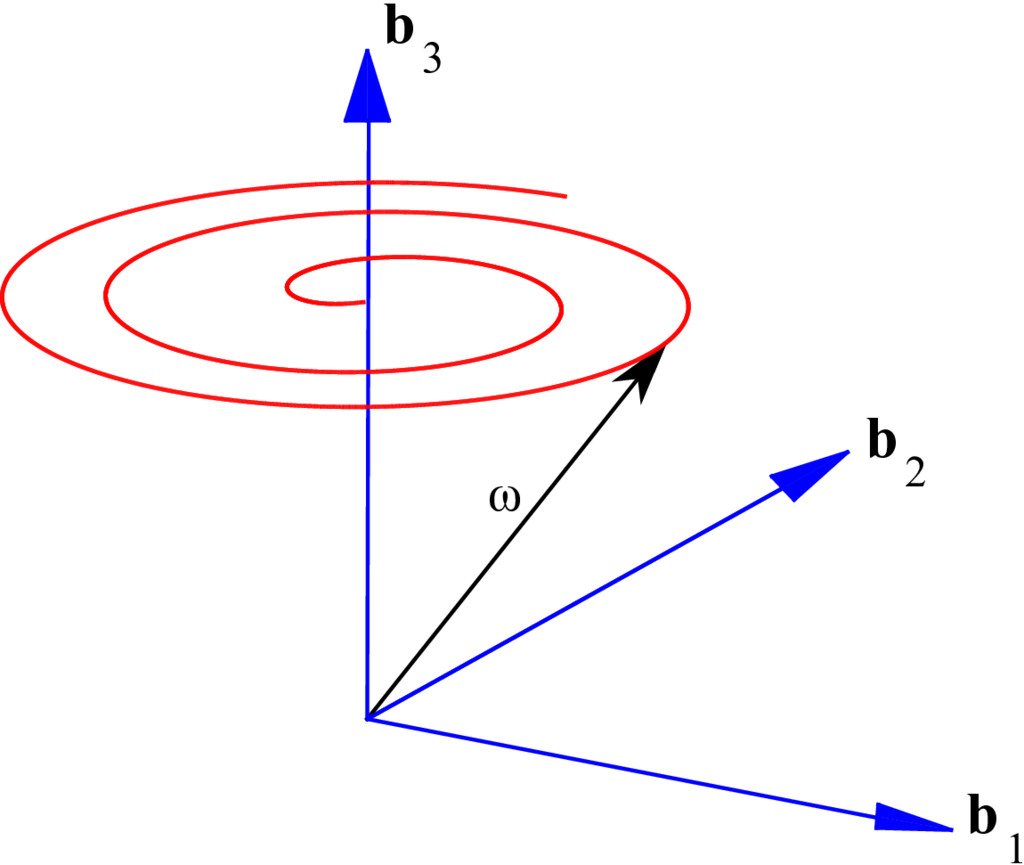
Fig. 4 Uniform burn: body surface.#
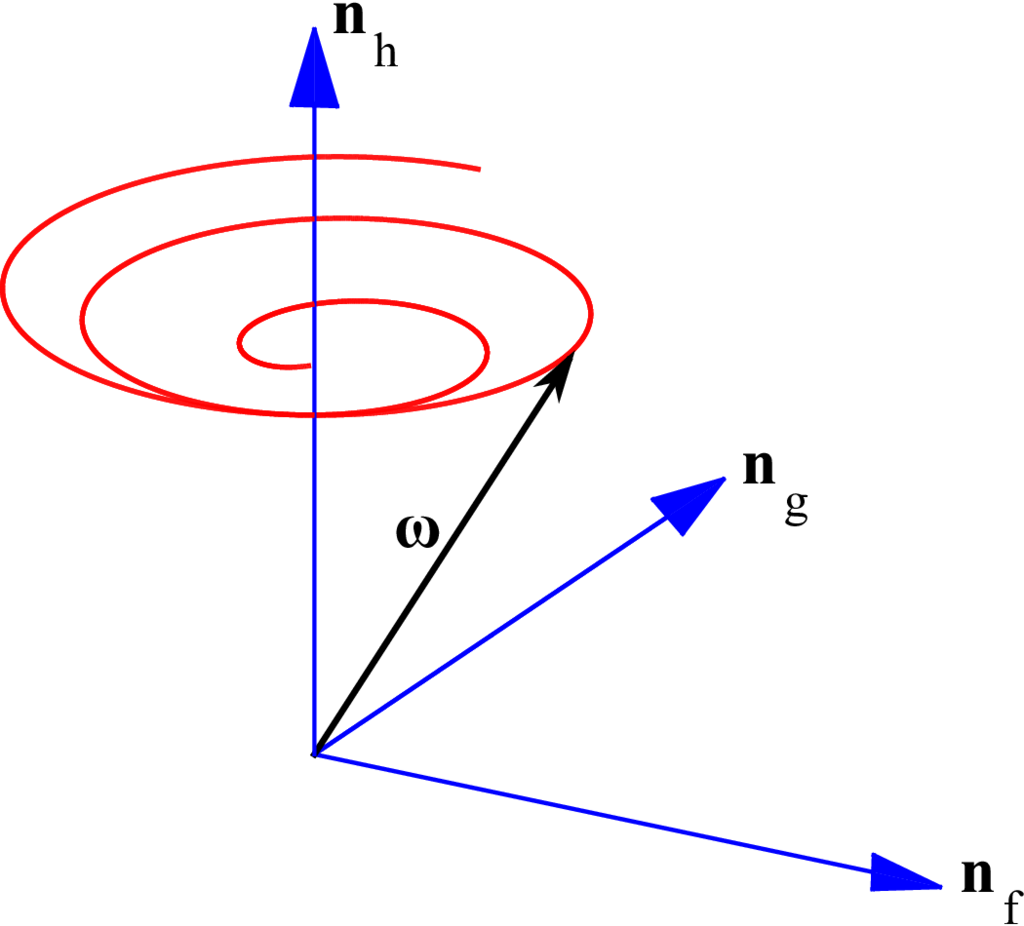
Fig. 5 Uniform burn: space surface.#
The rotation of \(\boldsymbol{\omega}\) in the inertial space (i.e., about \({\bf n}_h\) since it is inertially fixed) requires knowledge of the angle, \(\beta\), in Equation (40):
This angle also decays with time for the uniformly burning cylinder, effectively reducing the system’s motion to that of simple or pure spin, i.e., a motion in which the angular velocity and angular momentum vectors are parallel. The above expressions of \(\theta\), and \(\beta\) along with the angular velocity permit the construction of the space surface as shown in Figure Fig. 5. Note that \({\bf n}_f\), \({\bf n}_g\), and \({\bf n}_h\) represent a dextral set of unit vectors which are inertially fixed.
Simulation Results#
import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Define the global physical parameters for the variable mass system#
rho_ini = 1020
rho_exhaust = 0.002 * rho_ini
L = 1 # m
h = L / 2 # m
R = L # m
u = 5 # m/s
m_dot = -rho_exhaust * u * np.pi * R**2
w0 = 0.2 # rad/s
Initial angular rates#
w10 = 0 # rad/s
w20 = w0 # rad/s
w30 = 0.3 # rad/s
Initial mass properties#
mf0 = np.pi * R**2 * L * rho_ini # kg
I10 = mf0 * (R**2 / 4 + h**2 / 3) # kg*m^2
I30 = mf0 * R**2 / 2 # kg*m^2
chi0 = 0 # Initial precession angle
Fd0 = 0 # Initial F value
tb = -mf0 / m_dot - 1 # Burn time
Quaternion initial conditions (representing no initial rotation)#
q0 = [1, 0, 0, 0] # (w, x, y, z)
Combine initial conditions#
Y0 = [mf0, I10, I30, w10, w20, w30, chi0, Fd0] + q0
Define the differential equations#
def uniburn(t, w):
m, I1, I3, w1, w2, w3, chi, F, qw, qx, qy, qz = w
# Mass varying terms
md = -rho_exhaust * np.pi * R**2 * u # mass
I1d = md * (R**2 / 4 + h**2 / 3) # transverse moment of inertia
I3d = md * R**2 / 2 # spin moment of inertia
# Equations of motion for the axisymmetric cylinder undergoing uniform burn
w1d = (I1 - I3) * w2 * w3 / I1 - (I1d - md * (h**2 + R**2 / 4)) * w1 / I1
w2d = -(I1 - I3) * w1 * w3 / I1 - (I1d - md * (h**2 + R**2 / 4)) * w2 / I1
w3d = -(I3d - md * R**2 / 2) * w3
chid = (1 - I3 / I1) * w3
Fd = -(I1d - md * (h**2 + R**2 / 4)) / I1
# Quaternion derivative
omega_quat = np.array([0, w1, w2, w3])
quat = np.array([qw, qx, qy, qz])
quat_dot = 0.5 * np.array(quat_mult(quat, omega_quat))
wd = [md, I1d, I3d, w1d, w2d, w3d, chid, Fd, quat_dot[0], quat_dot[1], quat_dot[2], quat_dot[3]]
return wd
Function to multiply two quaternions#
def quat_mult(q, r):
w1, x1, y1, z1 = q
w2, x2, y2, z2 = r
return [
w1*w2 - x1*x2 - y1*y2 - z1*z2,
w1*x2 + x1*w2 + y1*z2 - z1*y2,
w1*y2 - x1*z2 + y1*w2 + z1*x2,
w1*z2 + x1*y2 - y1*x2 + z1*w2
]
Time span for the simulation#
dt = 0.01
t_eval = np.arange(0, tb, dt)
Solve the ODEs#
sol = solve_ivp(uniburn, [0, tb], Y0, t_eval=t_eval, atol=1e-9, rtol=1e-8)
# Extract results if the integration was successful
if sol.status == 0:
print("Integration successful.")
t = sol.t
m = sol.y[0]
I1 = sol.y[1]
I3 = sol.y[2]
omega1 = sol.y[3]
omega2 = sol.y[4]
omega3 = sol.y[5]
chi = sol.y[6]
F = sol.y[7]
qw, qx, qy, qz = sol.y[8], sol.y[9], sol.y[10], sol.y[11]
else:
print(f"Integration failed with status {sol.status}: {sol.message}")
# Print the final time to check if it reached the end of the burn time
print(f"Final time: {sol.t[-1]}")
Integration successful.
Final time: 99.0
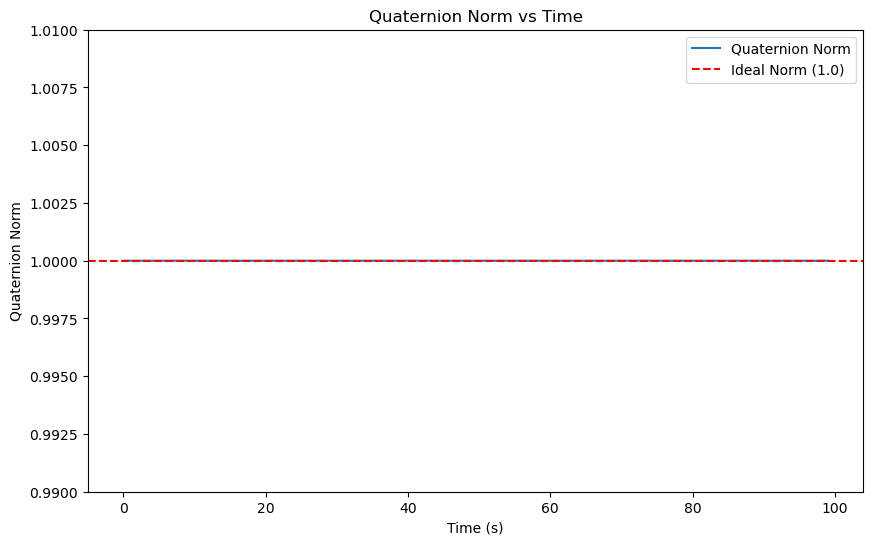
# Plot the quaternion norm over time
quat_norm = np.sqrt(qw**2 + qx**2 + qy**2 + qz**2)
norm_violation_indices = np.where(np.abs(quat_norm - 1) > 1e-6)[0]
if len(norm_violation_indices) > 0:
print(f"Quaternion constraint violated at time steps: {t[norm_violation_indices]}")
else:
print("Quaternion constraint satisfied throughout the simulation.")
plt.figure(figsize=(10, 6))
plt.plot(t, quat_norm, label='Quaternion Norm')
plt.axhline(y=1.0, color='r', linestyle='--', label='Ideal Norm (1.0)')
plt.xlabel('Time (s)')
plt.ylabel('Quaternion Norm')
plt.title('Quaternion Norm vs Time')
plt.ylim([0.99, 1.01]) # Adjust y-limits for better visualization
plt.legend()
plt.show()
Quaternion constraint satisfied throughout the simulation.
Function to convert quaternion to Euler angles (Z-X-Z sequence)#
def quat_to_euler_zxz(q):
"""
Convert a quaternion to Euler angles (Z-X-Z sequence).
"""
w, x, y, z = q
# Compute the Euler angles
psi = np.arctan2(2*(w*z + x*y), 1 - 2*(y**2 + z**2))
theta = np.arccos(2*(w*y - z*x))
phi = np.arctan2(2*(w*z + y*x), 1 - 2*(x**2 + y**2))
return psi, theta, phi
Extract Euler angles from quaternions#
psi, theta, phi = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
for i in range(len(qw)):
psi[i], theta[i], phi[i] = quat_to_euler_zxz([qw[i], qx[i], qy[i], qz[i]])
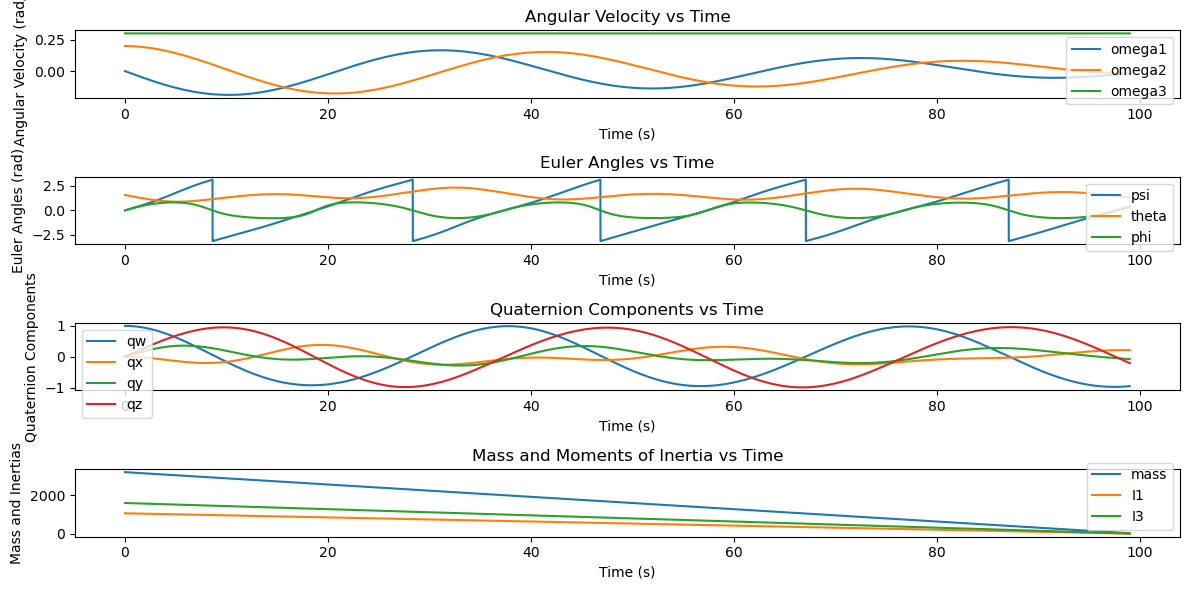
Plot the results#
plt.figure(figsize=(12, 6))
# Plot angular velocities
plt.subplot(4, 1, 1)
plt.plot(sol.t, omega1, label='omega1')
plt.plot(sol.t, omega2, label='omega2')
plt.plot(sol.t, omega3, label='omega3')
plt.xlabel('Time (s)')
plt.ylabel('Angular Velocity (rad/s)')
plt.title('Angular Velocity vs Time')
plt.legend()
# Plot Euler angles
plt.subplot(4, 1, 2)
plt.plot(sol.t, psi, label='psi')
plt.plot(sol.t, theta, label='theta')
plt.plot(sol.t, phi, label='phi')
plt.xlabel('Time (s)')
plt.ylabel('Euler Angles (rad)')
plt.title('Euler Angles vs Time')
plt.legend()
# Plot quaternions
plt.subplot(4, 1, 3)
plt.plot(sol.t, qw, label='qw')
plt.plot(sol.t, qx, label='qx')
plt.plot(sol.t, qy, label='qy')
plt.plot(sol.t, qz, label='qz')
plt.xlabel('Time (s)')
plt.ylabel('Quaternion Components')
plt.title('Quaternion Components vs Time')
plt.legend()
# Plot mass and moments of inertia
plt.subplot(4, 1, 4)
plt.plot(sol.t, m, label='mass')
plt.plot(sol.t, I1, label='I1')
plt.plot(sol.t, I3, label='I3')
plt.xlabel('Time (s)')
plt.ylabel('Mass and Inertias')
plt.title('Mass and Moments of Inertia vs Time')
plt.legend()
plt.tight_layout()
plt.show()
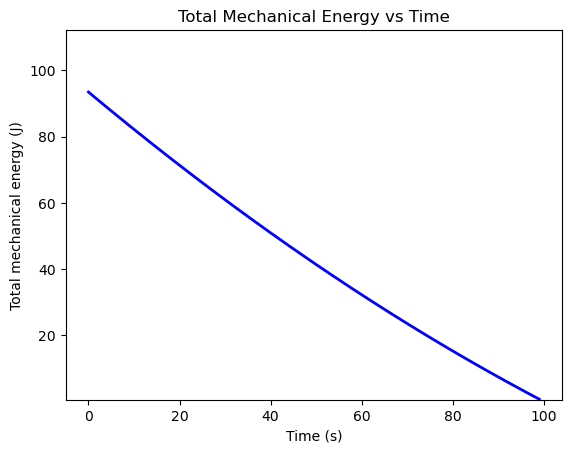
# Plot the T-handle's total mechanical energy over time
E = 0.5 * (I1 * omega1**2 + I1 * omega2**2 + I3 * omega3**2)
plt.figure()
plt.plot(sol.t, E, '-b', linewidth=2)
plt.xlabel('Time (s)')
plt.ylabel('Total mechanical energy (J)')
plt.ylim([min(E) * 0.8, max(E) * 1.2]) # Set fixed y-axis limits
plt.title('Total Mechanical Energy vs Time')
plt.show()
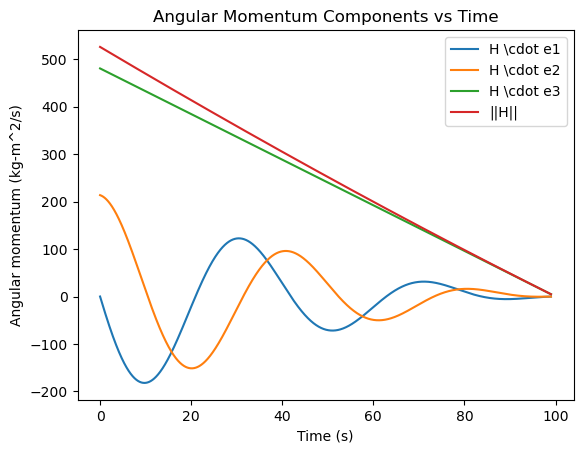
# Plot the components of the angular momentum about the mass center and the total angular momentum over time
H1 = I1 * omega1 # kg-m^2/s
H2 = I1 * omega2 # kg-m^2/s
H3 = I3 * omega3 # kg-m^2/s
H = np.sqrt(H1**2 + H2**2 + H3**2) # kg-m^2/s
plt.figure()
plt.plot(sol.t, H1, label='H \cdot e1')
plt.plot(sol.t, H2, label='H \cdot e2')
plt.plot(sol.t, H3, label='H \cdot e3')
plt.plot(sol.t, H, label='||H||')
plt.xlabel('Time (s)')
plt.ylabel('Angular momentum (kg-m^2/s)')
plt.title('Angular Momentum Components vs Time')
plt.legend()
plt.show()
# Function to convert quaternion to rotation matrix
def quat_to_rot_matrix(q):
"""
Convert a quaternion q to a rotation matrix.
"""
w, x, y, z = q
return np.array([
[1 - 2*(y**2 + z**2), 2*(x*y - z*w), 2*(x*z + y*w)],
[2*(x*y + z*w), 1 - 2*(x**2 + z**2), 2*(y*z - x*w)],
[2*(x*z - y*w), 2*(y*z + x*w), 1 - 2*(x**2 + y**2)]
])
def animate_t_handle_quat(qw, qx, qy, qz, dt):
# Specify dimensions for the T-handle
LAG = 0.5 # cm
LBC = 4 # cm
LAD = 2 # cm
# Initialize arrays to store the T-handle's orientation and key points
e1 = np.zeros((3, len(qw)))
e2 = np.zeros((3, len(qw)))
e3 = np.zeros((3, len(qw)))
xA, yA, zA = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
xB, yB, zB = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
xC, yC, zC = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
xD, yD, zD = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
# Calculate the orientation of the T-handle over time
for k in range(len(qw)):
q = [qw[k], qx[k], qy[k], qz[k]]
R = quat_to_rot_matrix(q)
e1[:, k] = R @ np.array([1, 0, 0])
e2[:, k] = R @ np.array([0, 1, 0])
e3[:, k] = R @ np.array([0, 0, 1])
xA[k] = -LAG * e2[0, k]
yA[k] = -LAG * e2[1, k]
zA[k] = -LAG * e2[2, k]
xB[k] = xA[k] + LBC / 2 * e1[0, k]
yB[k] = yA[k] + LBC / 2 * e1[1, k]
zB[k] = zA[k] + LBC / 2 * e1[2, k]
xC[k] = xA[k] - LBC / 2 * e1[0, k]
yC[k] = yA[k] - LBC / 2 * e1[1, k]
zC[k] = zA[k] - LBC / 2 * e1[2, k]
xD[k] = xA[k] + LAD * e2[0, k]
yD[k] = yA[k] + LAD * e2[1, k]
zD[k] = zA[k] + LAD * e2[2, k]
# Set up the figure window
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel('X (cm)')
ax.set_ylabel('Y (cm)')
ax.set_zlabel('Z (cm)')
ax.set_xlim([-LBC, LBC])
ax.set_ylim([-LBC, LBC])
ax.set_zlim([-LAD, LAD])
ax.set_title('T-handle Animation')
# Draw the T-handle
AD, = ax.plot([xA[0], xD[0]], [yA[0], yD[0]], [zA[0], zD[0]], 'k-', linewidth=5)
BC, = ax.plot([xB[0], xC[0]], [yB[0], yC[0]], [zB[0], zC[0]], 'k-', linewidth=5)
# Animate the T-handle's motion by updating the figure with its current orientation
def update(k):
AD.set_data([xA[k], xD[k]], [yA[k], yD[k]])
AD.set_3d_properties([zA[k], zD[k]])
BC.set_data([xB[k], xC[k]], [yB[k], yC[k]])
BC.set_3d_properties([zB[k], zC[k]])
return AD, BC,
ani = FuncAnimation(fig, update, frames=len(qw), interval=dt * 1000, blit=True)
plt.show()
# Example usage
# Assuming `qw`, `qx`, `qy`, `qz` are the quaternion components obtained from the previous solution
animate_t_handle_quat(qw, qx, qy, qz, dt)
