Equations of Motion and the Angular Velocity of an Axisymmetric Systems

Fig. 1 is of a general variable mass system. It comprises a consumable rigid base B and a fluid phase F. A massless shell C of constant volume \(V_0\) and constant surface area \(S_0\) is rigidly attached to B. It is assumed that mass can enter or exit C through the region represented as a dashed circle of radius \(R\). At every instant, the shell and everything within it is considered to be the system of interest.

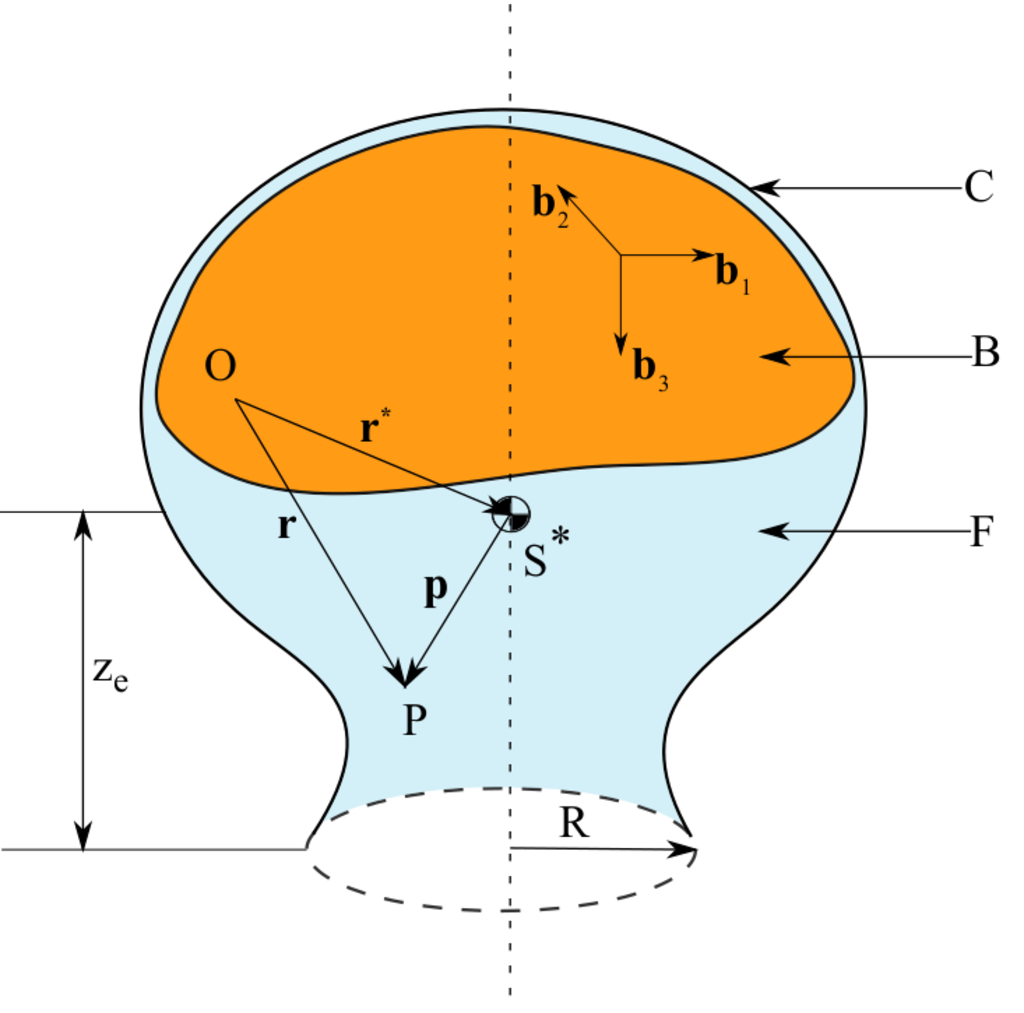
Fig. 1 General variable mass system.

The vector equation of attitude motion of such a system can be derived from the laws of mechanics (such as Newton-Euler equations, Lagrange’s method, etc.) and appropriately invoking Reynold’s Transport Theorem. This approach has been discussed in [Nanjangud and Eke, 2012]. The following is the equation of attitude motion of a general variable mass system:

(1)\[\begin{split}\mathbf{M}^* = \mathbf{I}^* \cdot \boldsymbol{\alpha} + \boldsymbol{\omega} \times (\mathbf{I}^* \cdot \boldsymbol{\omega}) + \frac{^B d \mathbf{I}^*}{dt} \cdot \boldsymbol{\omega} \\ + \int_{S_0} \rho \mathbf{[p \times (\boldsymbol{\omega} \times p)](v_r \cdot {n})} \, dS \\ + \int_{V_0} \rho \mathbf{[\boldsymbol{\omega} \times (p \times v_r)]} \, dV + \frac{^B d}{dt} \int_{V_0} \rho \mathbf{(p \times v_r)} \, dV \\ + \int_{S_0} \rho \mathbf{(p \times v_r)}(\mathbf{v_r} \cdot {\mathbf{n}}) \, dS\end{split}\]

Several other forms of the equation of attitude motion have been derived for a variable mass system in the literature. However, Equation (1) is most tractable for examining the attitude evolution as it is decoupled from the translational dynamics.

The volume integrals in Equation (1) are typically hard to evaluate in closed-form since the internal flow field is not generally known within a system. However, in the case of rockets, reasonable assumptions can be made about this internal flow. It is typically assumed that the internal flow of gases within a rocket relative to its casing is both steady and axisymmetric. Further assuming that the flow lacks a whirl component forces the last three terms of Equation (1) to disappear, making it less cumbersome. Thus, the equation of attitude motion becomes:

(2)\[\begin{split}\mathbf{M}^* = \mathbf{I}^* \cdot \boldsymbol{\alpha} + \boldsymbol{\omega} \times (\mathbf{I^*} \cdot \boldsymbol{\omega}) + \frac{^B d \mathbf{I}^*}{dt} \cdot \boldsymbol{\omega} \\ + \int_{S_0} \rho \mathbf{\big[p \times (\boldsymbol{\omega} \times p)\big](v_r \cdot {n})} \, dS\end{split}\]

The remainder of this paper concerns the torque-free motions of axisymmetric variable mass systems so \(\mathbf{M^* = 0}\). Note that though this non-whirling flow assumption is not realistic, it has been shown that the magnitude of the transverse angular rates are unaffected by such a flow assumption [Wang and Eke, 1995]. As stability information in this paper is derived from the magnitude of the angular rates, the non-whirling flow assumption is sufficient.

Referring back to Figure Fig. 1, \(\mathbf{b}_1\), \(\mathbf{b}_2\), \(\mathbf{b}_3\) are a dextral set of unit vectors affixed in B and parallel to its principal directions. The instantaneous central inertia dyadic of this axisymmetric system is:

(3)\[\mathbf{I}^* \triangleq I \, \mathbf{b}_1 \mathbf{b}_1 + I \, \mathbf{b}_2 \mathbf{b}_2 + J \, \mathbf{b}_3 \mathbf{b}_3\]

where \(I\) and \(J\) are the instantaneous central principal moments of inertia of the variable mass system. Note that the mass center, \(S^*\), is not necessarily fixed relative to B and is always located on the symmetry axis, parallel to \(\mathbf{b}_3\). Further, the inertial angular velocity of B at any instant is:

(4)\[\boldsymbol{\omega} \triangleq \omega_1 \mathbf{b}_1 + \omega_2 \mathbf{b}_2 + \omega_3 \mathbf{b}_3\]

and, as a result, the inertial angular acceleration is:

(5)\[\boldsymbol{\alpha} = \dot{\omega}_1 \mathbf{b}_1 + \dot{\omega}_2 \mathbf{b}_2 + \dot{\omega}_3 \mathbf{b}_3\]

The first three terms on the right-hand side of Equation (2) evaluate to:

(6)\[\mathbf{I}^* \cdot \boldsymbol{\alpha} = I \dot{\omega}_1 \mathbf{b}_1 + I \dot{\omega}_2 \mathbf{b}_2 + J \dot{\omega}_3 \mathbf{b}_3\]

(7)\[\boldsymbol{\omega} \times (\mathbf{I}^* \cdot \boldsymbol{\omega}) = (J - I)\omega_2 \omega_3 \mathbf{b}_1 - (J - I)\omega_1 \omega_3 \mathbf{b}_2\]

(8)\[\frac{^B d \mathbf{I}^*}{dt} \cdot \boldsymbol{\omega} = \dot{I} \omega_1 \mathbf{b}_1 + \dot{I} \omega_2 \mathbf{b}_2 + \dot{J} \omega_3 \mathbf{b}_3\]

The assumed steady symmetry of the internal fluid flow is further constrained to be uniform along the exit plane so that \(\mathbf{v_r \cdot n}= u = \text{constant}\), which then yields the following expression for the surface integral in Equation (2):

(9)\[\int_{S_0} \rho \mathbf{[p \times (\boldsymbol{\omega} \times p)](v_r \cdot {n})} \, dS = -\dot{m} \big[(z_e^2 + \frac{R^2}{4})(\omega_1 \mathbf{b}_1 + \omega_2 \mathbf{b}_2) + \frac{R^2}{2}\omega_3 \mathbf{b}_3 \big]\]

where \(\dot{m}\), the rate of mass loss, is given by:

(10)\[\dot{m} = -\rho_{exit} \pi R^2 u = \text{constant}\]

\(\rho_{exit}\) is the assumed density of exhaust gases on the exit plane.

Substituting Equations (6), (7), (8), and (9) into Equation (2) yields:

(11)\[\dot{\omega}_1 = \frac{I - J}{I} \omega_2 \omega_3 - \frac{1}{I} \big[\dot{I} - \dot{m}(z_e^2 + \frac{R^2}{4}) \big] \omega_1\]

(12)\[\dot{\omega}_2 = -\frac{I - J}{I} \omega_3 \omega_1 - \frac{1}{I} \big[\dot{I} - \dot{m}(z_e^2 + \frac{R^2}{4}) \big] \omega_2\]

(13)\[\dot{\omega}_3 = - \frac{1}{J} \big[\dot{J} - \dot{m}(\frac{R^2}{2}) \ \big] \omega_3\]

Equations (11) - (13) are the scalar equations of attitude motion for an axisymmetric, torque-free variable mass system with axisymmetric non-whirling internal mass flow. Equations (11) and (12) are commonly referred to as the equations of transverse attitude motion while Equation (13) is the spin equation of motion; \(\omega_1\) and \(\omega_2\) are transverse rates and \(\omega_3\) is the spin rate. The attitude motion of a variable system is characterized by solving these equations.

Spin rate

As the spin equation of motion is decoupled from the transverse equations of motion, an expression for the spin rate can be easily obtained and is given by

(14)\[\omega_3 = \omega_{30} \text{exp}(\Phi)\]

where

(15)\[\Phi = - \int_0^t \bigg[\bigg(\dot J - \dot m R^2/2\bigg)/J \bigg] \mathrm{d}t.\]

If \(J \triangleq m k_3^2\), where \(k_3\) is the time-varying axial radius of gyration, then \(\Phi\) evaluates to

(16)\[\Phi = \int_{m(0)}^{m} \frac{(R^2/2)}{k_3^2} \frac{\mathrm{d}m}{m} + \mathrm{ln}\bigg(\frac{J(0)}{J}\bigg).\]

Substituting for \(\Phi\) in Equation (14) gives the following expression for the spin rate

(17)\[\omega_3 = \omega_{30} \frac{J(0)}{J} \text{exp}\bigg(\int_{m(0)}^{m} \frac{(R^2/2)}{k_3^2} \frac{\mathrm{d}m}{m} \bigg)\]

Examining Equation (17), the spin rate may decay, stay constant, grow, or fluctuate. Another observation that can be added to this is that the spin rate retains the polarity of its initial condition; if the initial condition is positive, then the spin rate is always non-negative, and vice versa. Further analysis in this chapter assumes a positive value for the initial spin rate. Additionally, if \(k_3^2\) is assumed to be a constant in Equation (17), then

(18)\[\omega_3 = \omega_{30} \bigg( \frac{m(0)}{m}\bigg) ^{1 - \frac{R^2}{2k_3^2}}.\]

Equation (18) asserts that the spin rate cannot fluctuate for a system with constant axial radius of gyration; it can only grow or decay monotonically, or stay constant. It can then also be inferred that a time-varying axial radius of gyration can lead to fluctuations in the spin rate. Thus, the radius of gyration has a crucial effect on the spin rate. These comments on the spin rate are in agreement with the work of Snyder and Warner [Snyder and Warner, 1968], and Wang and Eke [Wang and Eke, 1995].

Transverse rate

The transverse angular speeds can be solved for in a variety of different ways. Defining a complex variable \(\omega_c\) as

(19)\[\omega_c \triangleq \omega_1 + j \omega_2\]

allows Equations (11) and (12) to be combined to yield a differential equation linear in \(\omega_c\):

(20)\[\dot{\omega}_c = \Bigg\{-j \frac{I - J}{I} \omega_3 - \frac{1}{I}\bigg[\dot{I} - \dot{m}(z_e^2 + \frac{R^2}{4})\bigg]\Bigg\} \omega_c.\]

Integrating Equation (20) yields

(21)\[{\omega}_c = \omega_{co} \cdot \Gamma \cdot \text{exp} \bigg(-j\chi\bigg)\]

where

(22)\[\Gamma = \text{exp} \bigg[ -\int_0^t \frac{1}{I}\bigg[\dot{I} - \dot{m}(z_e^2 + \frac{R^2}{4})\bigg] \mathrm{d}t \bigg]\]

and

(23)\[\chi = \int_0^t (1 - \frac{J}{I}) \omega_3 \mathrm{d}t.\]

A consequence of Equation (23) is

(24)\[\dot \chi = (1 - \frac{J}{I}) \omega_3\]

where \(\dot \chi\) has the units of angular speed.

From Equations (21) and (19), the transverse speeds are given by

(25)\[\omega_1 = \Gamma (\omega_{10} \cos\chi + \omega_{20}\sin\chi)\]

(26)\[\omega_2 = \Gamma(-\omega_{10}\sin\chi + \omega_{20}\cos\chi)\]

and are oscillatory in nature.

Further, a transverse angular velocity vector \(\boldsymbol{\omega}_{t}\) which lies in the plane made by the principal directions \(\mathbf{b}_1\) and \(\mathbf{b}_2\) can also be defined as

(27)\[\boldsymbol{\omega}_{t} \triangleq \omega_1 {\bf b}_1+ \omega_2 {\bf b}_2,\]

whose magnitude is

(28)\[\omega_{12} = ||\boldsymbol{\omega}_{t}||= \sqrt{\omega_1^2 + \omega_2^2} = \sqrt{\Gamma^2 (\omega_{10}^2 +\omega_{20}^2)} = \Gamma \omega_0\]

where \(\omega_0 \triangleq \sqrt{\omega_{10}^2 + \omega_{20}^2} = \text{constant}\). The principal directions may be chosen such that \(\omega_{10} = 0\) and \(\omega_{20} = \omega_0\). This simplifies the appearance of the solutions in Equations (25) and (26) to

(29)\[\omega_1 = \omega_0 \Gamma \sin\chi\]

(30)\[\omega_2 = \omega_0 \Gamma \cos\chi.\]

Equation (27) can then be written as

(31)\[\boldsymbol{\omega}_{t} = \omega_0 \Gamma[\sin\chi {\bf b}_1+ \cos\chi {\bf b}_2] = \omega_0 \Gamma{\bf b}_{12} = \omega_{12} {\bf b}_{12},\]

where \({\bf b}_{12} = \sin\chi {\bf b}_1+ \cos\chi {\bf b}_2\); \({\bf b}_{12}\) is clearly a unit vector that is orthogonal to \({\bf b}_3\). These developments concerning the transverse angular velocity vector will be useful in developments in Section 3 on the geometry of motion.

From examining Equations (31) and (22), it is evident that the spin rate has no influence on the magnitude of the transverse angular velocity. Further, it shows that the magnitude of the transverse angular velocity vector is a rescaling of \(\omega_0\) by \(\Gamma\), a function of time that can either grow, decay, or fluctuate. \({\bf b}_{12}\) is a unit vector that rotates in the plane of \({\bf b}_1\) and \({\bf b}_2\) at the angular speed \(\dot \chi\). As revealed by Equation (24), \(\dot \chi\) may be positive or negative (assuming that \(\omega_3\) is always positive), depending on the relative values of \(k_1\) and \(k_3\); if \(k_3 > k_1\), then \({\bf b}_{12}\) rotates negatively in the body, advancing from \({\bf b}_1\) to \(-{\bf b}_2\) and around; if \(k_1 > k_3\), then \({\bf b}_{12}\) rotates positively in the body, coinciding with \({\bf b}_1\) and then with \({\bf b}_2\) and so on. As the interest of this paper is in understanding the nutational stability, no attempt is made to obtain an analytical expression for \(\chi\). Its value can be obtained numerically from Equation (23).

An expression for \(\Gamma\) can be developed involving the system’s transverse radius of gyration, \(k_1\). If \(I \triangleq m k_1^2\), \(\Gamma\) may be reformulated in Equation (22) as

\[\Gamma = \frac{I(0)}{I}\text{exp}\bigg[ \int_{m(0)}^m \frac{\bigg[z_e^2 + \frac{R^2}{4}\bigg]}{k_1^2} \frac{\mathrm{d}m}{m}\bigg]\]

Here, \(R\) is the constant radius of the exit plane while \(k_1\) and \(z_e\) can vary; these are parameters that are modeling constraints. Substituting for \(\Gamma\) into Equation (28) yields the following expression for the magnitude of the transverse angular velocity:

(32)\[\omega_{12} = \omega_{0} \bigg(\frac{I(0)}{I}\bigg) \text{exp}\bigg[ \int_{m(0)}^m \frac{\bigg[z_e^2 + \frac{R^2}{4}\bigg]}{k_1^2} \frac{\mathrm{d}m}{m}\bigg].\]

Some of the effects of the variations in \(z_e\) and \(k_1\) on the transverse rate will be studied in the subsequent passage on variable mass cylinders. However, it should be evident that \(\omega_{12}\) can grow, decay, or fluctuate but under no circumstance is it constant for an axisymmetric variable mass system.

Finally, the inertial angular velocity of an axisymmetric variable mass system can now be written as

(33)\[\boldsymbol{\omega} = \omega_0 \Gamma{\bf b}_{12} + \omega_3 {\bf b}_3,\]

the form of which mimics the constant-mass rigid body case, for which \(\Gamma = 1\).