End Burn

Theory

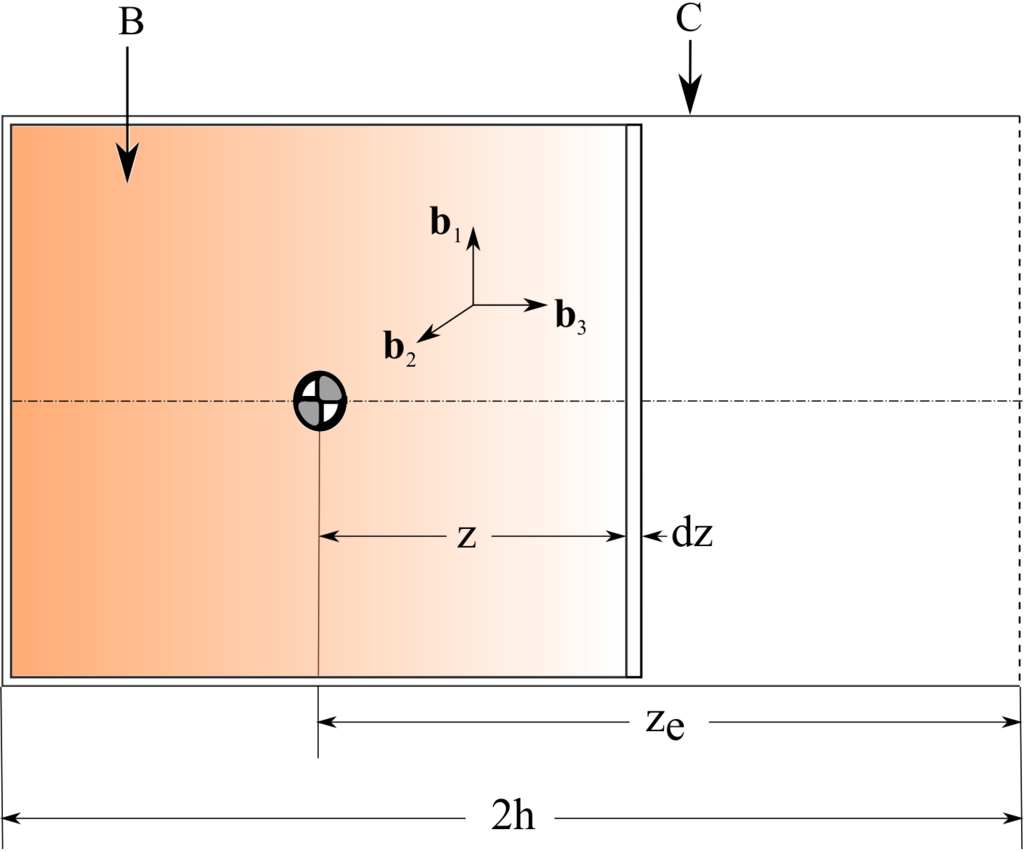
Fig. 6 End burning cylinder.

In this mechanism of mass variation, the cylinder burns from the circular face closest to the exit plane towards its other face. At any instant, the unburned part retains the shape of a right circular cylinder. Figure Fig. 6 represents a cylinder that burns from right to left. The axial radius of gyration for such a cylinder is constant, given by \(k_3^2 = \frac{R^2}{4}\). The corresponding axial moment of inertia is

(45)\[J = m \frac{R^2}{4}\]

As in the case of uniform burn, the spin rate can thus be determined from Equation (18) to be constant,

(46)\[\omega_3 = \omega_{30}.\]

The more interesting development occurs in the transverse directions. The transverse radius of gyration is \(k_1^2 = \frac{R^2}{4} + \frac{z^2}{3}\). Due to the changing length of the cylinder, \(k_1\) is not a constant. Then, the transverse moment of inertia is

(47)\[I = m\left(\frac{R^2}{4} + \frac{z^2}{3}\right)\]

If \(z\) is the instantaneous half length of the unburned cylinder, then its instantaneous mass is given by

(48)\[m = \pi R^2 (2z)\]

The rate of mass loss is then

(49)\[\dot m = 2 \pi R^2 \dot z.\]

which can also be written as

(50)\[\mathrm{d}m = 2 \pi R^2 \mathrm{d}z.\]

From Equations (48) and (50), it is possible to recast Equation (32) as

(51)\[\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \text{exp}\left[ \int_{z_0}^z \frac{\left[z_e^2 + \frac{R^2}{4}\right]} {\frac{R^2}{4} + \frac{z^2}{3}} \frac{\mathrm{d}z}{z}\right].\]

Substituting \(z_e = 2h - z\) into Equation (51) gives

(52)\[\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \text{exp}\left[ \int_{z_0}^z \frac{\left[z^2 + 4h^2 -4hz + \frac{R^2}{4}\right]} {\frac{R^2}{4} + \frac{z^2}{3}} \frac{\mathrm{d}z}{z}\right]\]

which can also be reformulated as

(53)\[\begin{split}\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \text{exp}\left[ \int_{z_0}^z \frac{3z - 12h}{\frac{3R^2}{4} + z^2} \mathrm{d}z \nonumber\\ + \left(12h^2 + \frac{3R^2}{4} \right)\int_{z_0}^z \frac{\mathrm{d}z} {z\left(\frac{3R^2}{4} + z^2\right)} \right].\end{split}\]

A partial fraction expansion of the second integral in Equation (53) then gives

(54)\[\begin{split}\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \text{exp}\left[ \int_{z_0}^z\frac{3z - 12h} {\frac{3R^2}{4} + z^2} \mathrm{d}z \nonumber\\ + \left(\frac{16h^2}{R^2} + 1 \right) \int_{z_0}^z \left(\frac{1}{z} - \frac{z} {\frac{3R^2}{4} + z^2}\right) \mathrm{d}z \right]\end{split}\]

or, after some algebra,

(55)\[\begin{split}\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \text{exp}\left[ -\int_{z_0}^z \frac{12h}{ \frac{3R^2}{4} + z^2 } \mathrm{d}z \nonumber \\ - \left(\frac{16h^2}{R^2} - 2 \right) \int_{z_0}^z \frac{z}{\frac{3R^2}{4} + z^2} \mathrm{d}z\nonumber\\ + \left(\frac{16h^2}{R^2} + 1 \right) \int_{z_0}^z\frac{\mathrm{d}z}{z} \right].\end{split}\]

The solution to the transverse rate is

\[\begin{split}\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \text{exp}\left[ \frac{8 \sqrt{3}h}{R} \tan^{-1}\left( \frac{2\sqrt{3}R(z-h)}{3R^2 + 4zh} \right) \nonumber\\ - \left(\frac{8h^2}{R^2} - 1 \right) \log\left( \frac{\frac{3R^2}{4} + z^2} {\frac{3R^2}{4} + h^2}\right) \nonumber\\ + \left(\frac{16h^2}{R^2} + 1 \right) \log\left(\frac{z}{h}\right) \right].\end{split}\]

which can also be expressed as

\[\begin{split}\omega_{12} = \omega_0 \left(\frac{I(0)}{I}\right) \left( \frac{\frac{3R^2}{4} + h^2} {\frac{3R^2}{4} + z^2}\right)^{ \left(\frac{8h^2}{R^2} - 1 \right)} \left(\frac{z}{h}\right)^ {\left(\frac{16h^2}{R^2} + 1 \right)} \nonumber\\ \text{exp}\left[\frac{8 \sqrt{3}h}{R} \tan^{-1}\left( \frac{2\sqrt{3}R(z-h)}{3R^2 + 4zh} \right) \right].\end{split}\]

The above solution can also be expressed in terms of the transverse radius of gyration as

(56)\[\begin{split}\omega_{12} = \omega_0 \left(\frac{k_1(0)}{k_1}\right)^{\frac{8h^2}{R^2}} \left(\frac{z}{h}\right)^{\frac{16h^2}{R^2}}\nonumber\\ \text{exp}\left[\frac{8 \sqrt{3}h}{R} \tan^{-1}\left( \frac{2\sqrt{3}R(z-h)}{3R^2 + 4zh} \right) \right].\end{split}\]

Equation (56) explains that, for an end burning cylinder, the transverse rate is regulated by 3 time-varying functions: the ratio of the initial transverse radius of gyration to its instantaneous value, the ratio of the instantaneous half length to the initial half length, and an exponential function. The first of these functions grows as the burn progresses but is always bounded as its denominator is never zero. The latter two functions, however, always decay with time. Thus, irrespective of the nature of the cylinder, the transverse rates for the end burn are always decaying; the rate of decay is seen to be faster for prolate cylinders when compared to oblate cylinders, which makes sense in view of Equation (56). This has also been observed in Reference [Eke and Wang, 1995].

The nutation angle for an end-burning cylinder is given by

(57)\[\theta(t) = \tan^{-1}( K k_1^2 \Gamma(t) ),\]

where \(K = \frac{\omega_0}{k_3^2 \omega_{30}}=\) constant. As both \(\Gamma(t)\) and \(k_1\) are generally decreasing with time, the nutation angle decays with time for any end burning cylinder. In other words, jet damping is observed for such a mass-varying cylinder. Figures Fig. 7 and Fig. 8 show the body and space surfaces for end burning cylinders where the \(J_0 > I_0\) (initial \(L = 1\) m and \(R = 0.8\) m) whereas Figures Fig. 9 and Fig. 10 are for end-burning cylinders where \(J_0 < I_0\) (initial \(L = 1\) m and \(R = 0.5\) m). It is interesting to note in the second case (where \(J_0 < I_0\)) that the angular velocity vector changes its direction of rotation, about both \({\bf b}_3\) and \({\bf n}_h\). Initially, it rotates in a clockwise direction and then switches to a counterclockwise direction, eventually converging to a pure spin about \({\bf b}_3\) in the body frame and \({\bf n}_h\) in the inertial frame. This transition point occurs when the ratio of the axial radius of gyration to the transverse radius of gyration falls below 1 and changes the sign of \(\dot \chi\) as given by Equation (24). In either case, the end burn is seen to exhibit a decay in the cone angle and is thus nutationally stable.

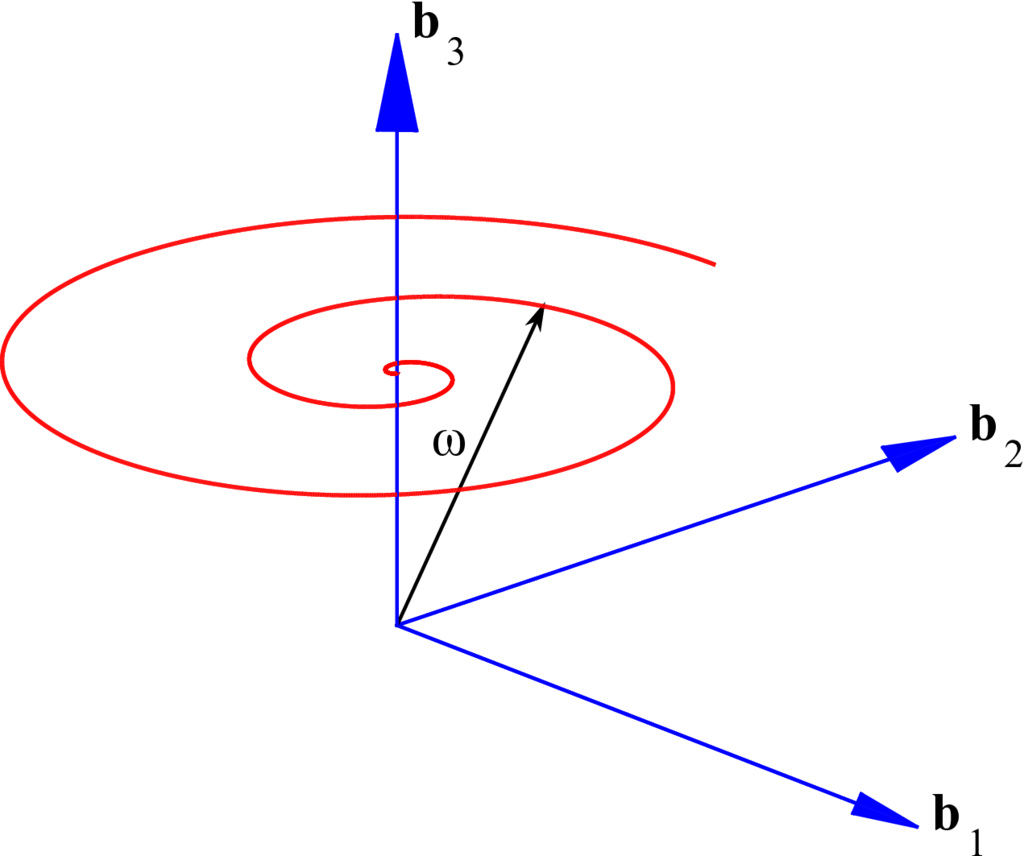
Fig. 7 End burn: body surface (\(J_0 > I_0\)).

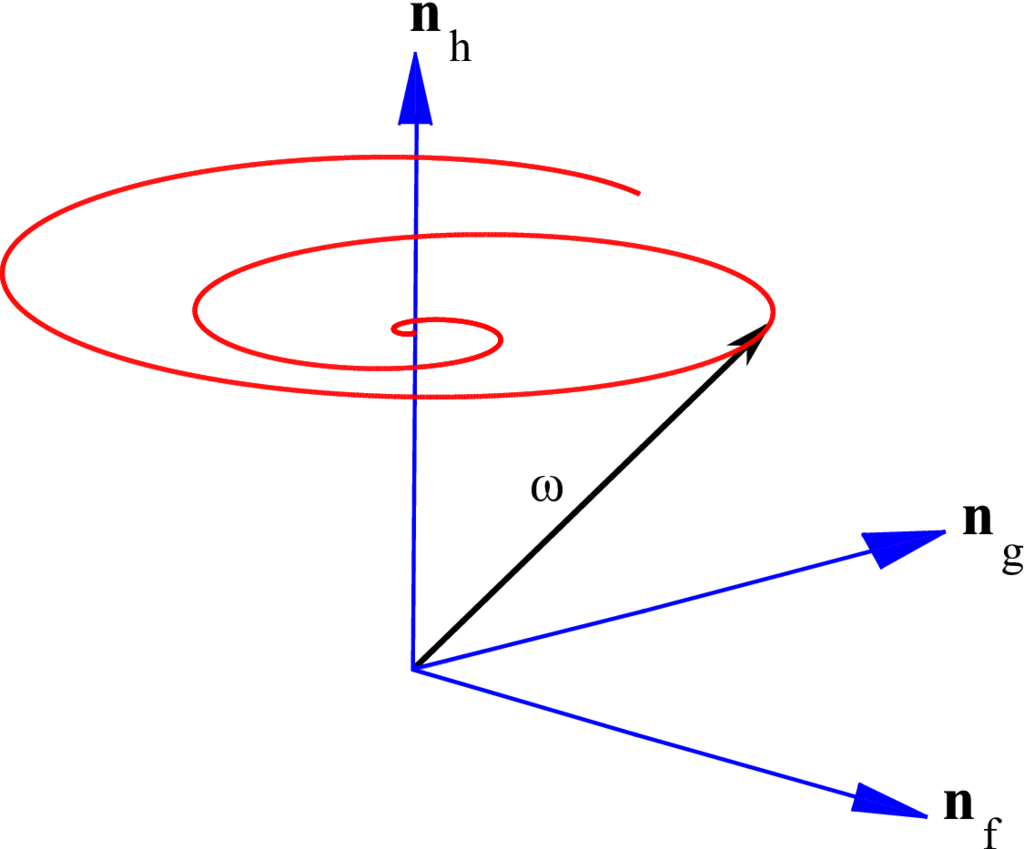
Fig. 8 End burn: space surface (\(J_0 > I_0\)).

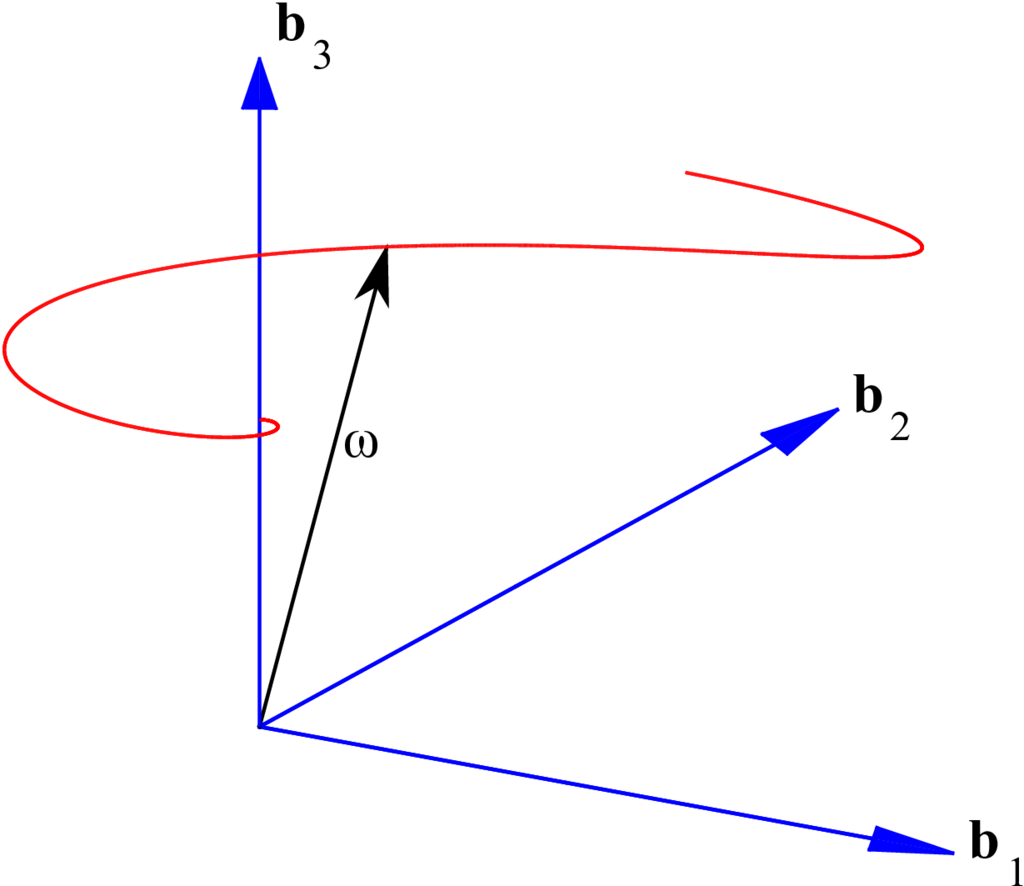
Fig. 9 End burn: body surface (\(J_0 < I_0\)).

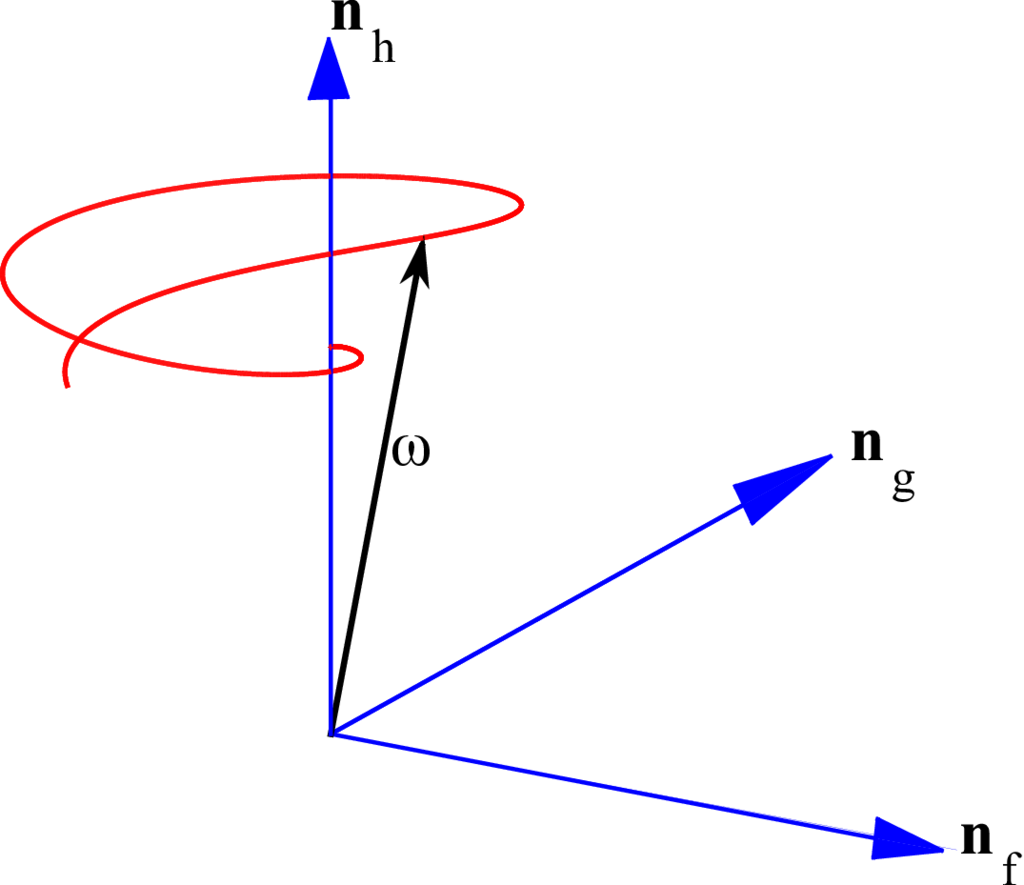
Fig. 10 End burn: space surface (\(J_0 < I_0\)).

Simulation Results

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.

Define the global physical parameters for the variable mass system

rho_ini = 1000
L = 1  # m
h = L / 2
z0 = h
R = 0.8 * L  # m
w0 = 0.2

Initial angular rates

w10 = 0  # rad/s
w20 = w0  # rad/s
w30 = 0.3  # rad/s

Initial mass properties

mf0 = np.pi * R**2 * L * rho_ini  # kg
I10 = mf0 * (R**2 / 4 + h**2 / 3)  # kg*m^2
I30 = mf0 * R**2 / 2  # kg*m^2
Theta0 = 0
F0 = 0
tb = 100  # s
m_dot = -mf0 / tb
z_dot = m_dot / (2 * rho_ini * np.pi * R**2)

Quaternion initial conditions (representing no initial rotation)

q0 = [1, 0, 0, 0]  # (w, x, y, z)

Combine initial conditions

Y0 = [mf0, I10, I30, w10, w20, w30, Theta0, F0, z0] + q0

Define the differential equations

def endburn(t, w):
    m, I1, I3, w1, w2, w3, Theta, F, z, qw, qx, qy, qz = w

    # Mass varying terms
    md = m_dot
    I1d = md * (R**2 / 4 + z**2)
    I3d = md * R**2 / 2

    # Distance of mass center from exit plane
    ze = 2 * h - z

    # Equations of motion for the axisymmetric cylinder undergoing uniform burn
    w1d = (I1 - I3) * w2 * w3 / I1 - (I1d - md * (ze**2 + R**2 / 4)) * w1 / I1
    w2d = -(I1 - I3) * w1 * w3 / I1 - (I1d - md * (ze**2 + R**2 / 4)) * w2 / I1
    w3d = -(I3d - md * R**2 / 2) * w3 / I3
    Thetad = (1 - I3 / I1) * w3
    Fd = -(I1d - md * (ze**2 + R**2 / 4)) / I1
    zd = md / m * z

    # Quaternion derivative
    omega_quat = np.array([0, w1, w2, w3])
    quat = np.array([qw, qx, qy, qz])
    quat_dot = 0.5 * np.array(quat_mult(quat, omega_quat))

    # Normalize quaternion to prevent drift
    quat_norm = np.linalg.norm(quat)
    if quat_norm > 0:
#         print("resetting the norm because it is", quat_norm)
        quat /= quat_norm

    wd = [md, I1d, I3d, w1d, w2d, w3d, Thetad, Fd, zd] + quat_dot.tolist()

    return wd

Function to multiply two quaternions

def quat_mult(q, r):
    """
    Multiply two quaternions q and r.
    """
    w1, x1, y1, z1 = q
    w2, x2, y2, z2 = r
    return [
        w1*w2 - x1*x2 - y1*y2 - z1*z2,
        w1*x2 + x1*w2 + y1*z2 - z1*y2,
        w1*y2 - x1*z2 + y1*w2 + z1*x2,
        w1*z2 + x1*y2 - y1*x2 + z1*w2
    ]

Time span for the simulation

dt = 0.01
t_eval = np.arange(0, tb-1, dt)

Solve the ODEs

sol = solve_ivp(endburn, [0, tb], Y0, t_eval=t_eval, atol=1e-9, rtol=1e-8)

# Check if the integration was successful
if sol.status == 0:
    print("Integration successful.")
else:
    print(f"Integration failed with status {sol.status}: {sol.message}")

# Print the final time to check if it reached the end of the burn time
print(f"Final time: {sol.t[-1]}")

# Extract results
t = sol.t
m = sol.y[0]
I1 = sol.y[1]
I3 = sol.y[2]
omega1 = sol.y[3]
omega2 = sol.y[4]
omega3 = sol.y[5]
Theta = sol.y[6]
F = sol.y[7]
z = sol.y[8]
qw, qx, qy, qz = sol.y[9], sol.y[10], sol.y[11], sol.y[12]

# Compute the quaternion norm and check for violations
quat_norm = np.sqrt(qw**2 + qx**2 + qy**2 + qz**2)
norm_violation_indices = np.where(np.abs(quat_norm - 1) > 1e-6)[0]

if len(norm_violation_indices) > 0:
    print(f"Quaternion constraint violated at time steps: {t[norm_violation_indices]}")
else:
    print("Quaternion constraint satisfied throughout the simulation.")

Integration failed with status -1: Required step size is less than spacing between numbers.
Final time: 98.99000000000001
Quaternion constraint satisfied throughout the simulation.

Compute the quaternion norm and check for violations

quat_norm = np.sqrt(qw**2 + qx**2 + qy**2 + qz**2)
norm_violation_indices = np.where(np.abs(quat_norm - 1) > 1e-6)[0]

if len(norm_violation_indices) > 0:
    print(f"Quaternion constraint violated at time steps: {t[norm_violation_indices]}")
else:
    print("Quaternion constraint satisfied throughout the simulation.")

Quaternion constraint satisfied throughout the simulation.

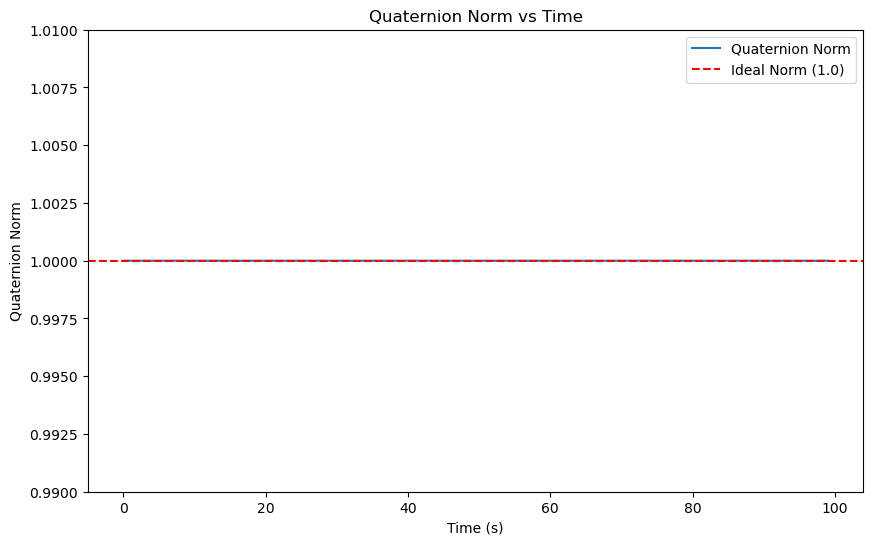
# Plot the quaternion norm over time
plt.figure(figsize=(10, 6))
plt.plot(t, quat_norm, label='Quaternion Norm')
plt.axhline(y=1.0, color='r', linestyle='--', label='Ideal Norm (1.0)')
plt.xlabel('Time (s)')
plt.ylabel('Quaternion Norm')
plt.title('Quaternion Norm vs Time')
plt.ylim([0.99, 1.01])  # Adjust y-limits for better visualization
plt.legend()
plt.show()

Function to convert quaternion to Euler angles (Z-X-Z sequence)

def quat_to_euler_zxz(q):
    """
    Convert a quaternion to Euler angles (Z-X-Z sequence).
    """
    w, x, y, z = q
    # Compute the Euler angles
    psi = np.arctan2(2*(w*z + x*y), 1 - 2*(y**2 + z**2))
    theta = np.arccos(2*(w*y - z*x))
    phi = np.arctan2(2*(w*z + y*x), 1 - 2*(x**2 + y**2))
    return psi, theta, phi

Extract Euler angles from quaternions

psi, theta, phi = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
for i in range(len(qw)):
    psi[i], theta[i], phi[i] = quat_to_euler_zxz([qw[i], qx[i], qy[i], qz[i]])

Plot the results

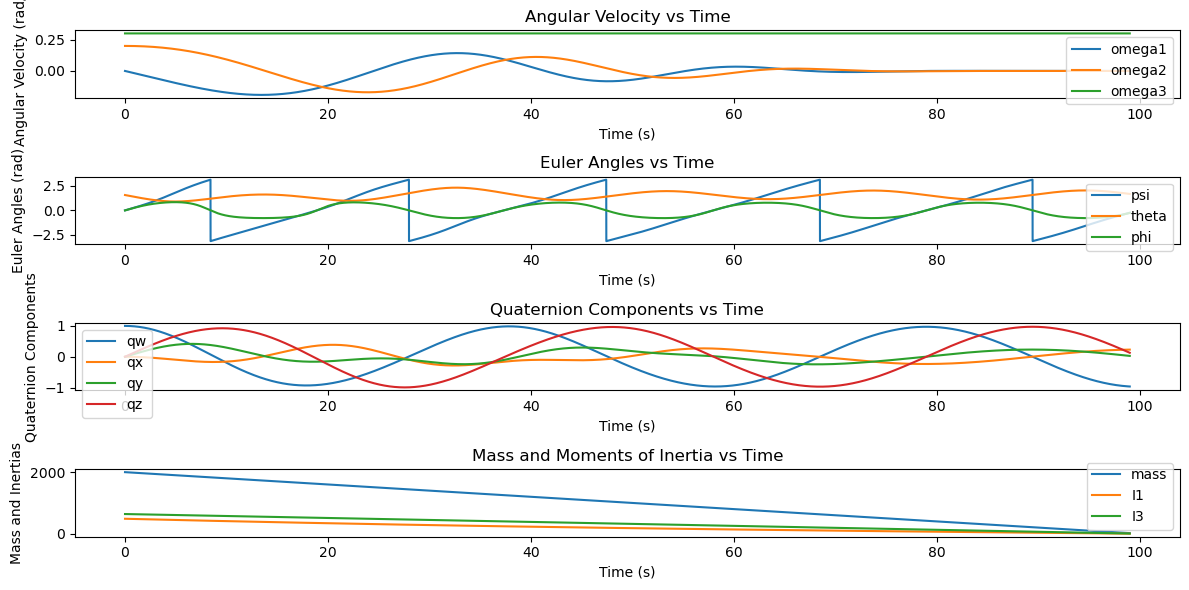
plt.figure(figsize=(12, 6))

# Plot angular velocities
plt.subplot(4, 1, 1)
plt.plot(sol.t, omega1, label='omega1')
plt.plot(sol.t, omega2, label='omega2')
plt.plot(sol.t, omega3, label='omega3')
plt.xlabel('Time (s)')
plt.ylabel('Angular Velocity (rad/s)')
plt.title('Angular Velocity vs Time')
plt.legend()

# Plot Euler angles
plt.subplot(4, 1, 2)
plt.plot(sol.t, psi, label='psi')
plt.plot(sol.t, theta, label='theta')
plt.plot(sol.t, phi, label='phi')
plt.xlabel('Time (s)')
plt.ylabel('Euler Angles (rad)')
plt.title('Euler Angles vs Time')
plt.legend()

# Plot quaternions
plt.subplot(4, 1, 3)
plt.plot(sol.t, qw, label='qw')
plt.plot(sol.t, qx, label='qx')
plt.plot(sol.t, qy, label='qy')
plt.plot(sol.t, qz, label='qz')
plt.xlabel('Time (s)')
plt.ylabel('Quaternion Components')
plt.title('Quaternion Components vs Time')
plt.legend()

# Plot mass and moments of inertia
plt.subplot(4, 1, 4)
plt.plot(sol.t, m, label='mass')
plt.plot(sol.t, I1, label='I1')
plt.plot(sol.t, I3, label='I3')
plt.xlabel('Time (s)')
plt.ylabel('Mass and Inertias')
plt.title('Mass and Moments of Inertia vs Time')
plt.legend()

plt.tight_layout()
plt.show()

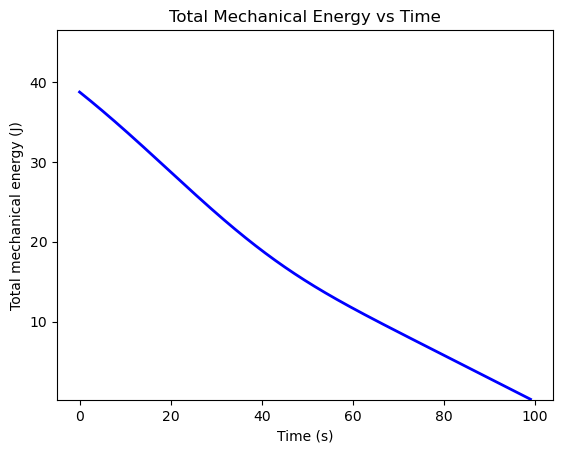
# Plot the T-handle's total mechanical energy over time
E = 0.5 * (I1 * omega1**2 + I1 * omega2**2 + I3 * omega3**2)

plt.figure()
plt.plot(sol.t, E, '-b', linewidth=2)
plt.xlabel('Time (s)')
plt.ylabel('Total mechanical energy (J)')
plt.ylim([min(E) * 0.8, max(E) * 1.2])  # Set fixed y-axis limits
plt.title('Total Mechanical Energy vs Time')
plt.show()

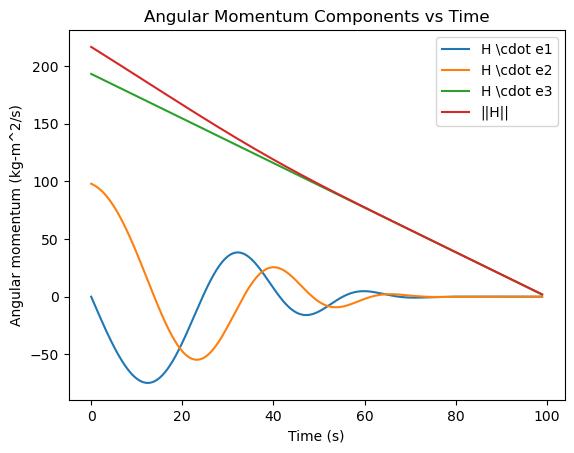
# Plot the components of the angular momentum about the mass center and the total angular momentum over time
H1 = I1 * omega1  # kg-m^2/s
H2 = I1 * omega2  # kg-m^2/s
H3 = I3 * omega3  # kg-m^2/s
H = np.sqrt(H1**2 + H2**2 + H3**2)  # kg-m^2/s

plt.figure()
plt.plot(sol.t, H1, label='H \cdot e1')
plt.plot(sol.t, H2, label='H \cdot e2')
plt.plot(sol.t, H3, label='H \cdot e3')
plt.plot(sol.t, H, label='||H||')
plt.xlabel('Time (s)')
plt.ylabel('Angular momentum (kg-m^2/s)')
plt.title('Angular Momentum Components vs Time')
plt.legend()
plt.show()

# Function to convert quaternion to rotation matrix
def quat_to_rot_matrix(q):
    """
    Convert a quaternion q to a rotation matrix.
    """
    w, x, y, z = q
    return np.array([
        [1 - 2*(y**2 + z**2), 2*(x*y - z*w), 2*(x*z + y*w)],
        [2*(x*y + z*w), 1 - 2*(x**2 + z**2), 2*(y*z - x*w)],
        [2*(x*z - y*w), 2*(y*z + x*w), 1 - 2*(x**2 + y**2)]
    ])

def animate_t_handle_quat(qw, qx, qy, qz, dt):
    # Specify dimensions for the T-handle
    LAG = 0.5  # cm
    LBC = 4  # cm
    LAD = 2  # cm

    # Initialize arrays to store the T-handle's orientation and key points
    e1 = np.zeros((3, len(qw)))
    e2 = np.zeros((3, len(qw)))
    e3 = np.zeros((3, len(qw)))
    xA, yA, zA = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
    xB, yB, zB = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
    xC, yC, zC = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))
    xD, yD, zD = np.zeros(len(qw)), np.zeros(len(qw)), np.zeros(len(qw))

    # Calculate the orientation of the T-handle over time
    for k in range(len(qw)):
        q = [qw[k], qx[k], qy[k], qz[k]]
        R = quat_to_rot_matrix(q)
        e1[:, k] = R @ np.array([1, 0, 0])
        e2[:, k] = R @ np.array([0, 1, 0])
        e3[:, k] = R @ np.array([0, 0, 1])
        xA[k] = -LAG * e2[0, k]
        yA[k] = -LAG * e2[1, k]
        zA[k] = -LAG * e2[2, k]
        xB[k] = xA[k] + LBC / 2 * e1[0, k]
        yB[k] = yA[k] + LBC / 2 * e1[1, k]
        zB[k] = zA[k] + LBC / 2 * e1[2, k]
        xC[k] = xA[k] - LBC / 2 * e1[0, k]
        yC[k] = yA[k] - LBC / 2 * e1[1, k]
        zC[k] = zA[k] - LBC / 2 * e1[2, k]
        xD[k] = xA[k] + LAD * e2[0, k]
        yD[k] = yA[k] + LAD * e2[1, k]
        zD[k] = zA[k] + LAD * e2[2, k]

    # Set up the figure window
    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    ax.set_xlabel('X (cm)')
    ax.set_ylabel('Y (cm)')
    ax.set_zlabel('Z (cm)')
    ax.set_xlim([-LBC, LBC])
    ax.set_ylim([-LBC, LBC])
    ax.set_zlim([-LAD, LAD])
    ax.set_title('T-handle Animation')

    # Draw the T-handle
    AD, = ax.plot([xA[0], xD[0]], [yA[0], yD[0]], [zA[0], zD[0]], 'k-', linewidth=5)
    BC, = ax.plot([xB[0], xC[0]], [yB[0], yC[0]], [zB[0], zC[0]], 'k-', linewidth=5)

    # Animate the T-handle's motion by updating the figure with its current orientation
    def update(k):
        AD.set_data([xA[k], xD[k]], [yA[k], yD[k]])
        AD.set_3d_properties([zA[k], zD[k]])
        BC.set_data([xB[k], xC[k]], [yB[k], yC[k]])
        BC.set_3d_properties([zB[k], zC[k]])
        return AD, BC,

    ani = FuncAnimation(fig, update, frames=len(qw), interval=dt * 1000, blit=True)
    plt.show()

# Example usage
# Assuming `qw`, `qx`, `qy`, `qz` are the quaternion components obtained from the previous solution
animate_t_handle_quat(qw, qx, qy, qz, dt)