Translational and Rotational Kinetics

Prepared by: Joost Hubbard, and Angadh Nanjangud

In this lecture we aim to cover the following topics:

1. Translational and Rotational Kinetics of a Rigid Body

Translational and Rotational Kinetics of a Rigid Body

Important

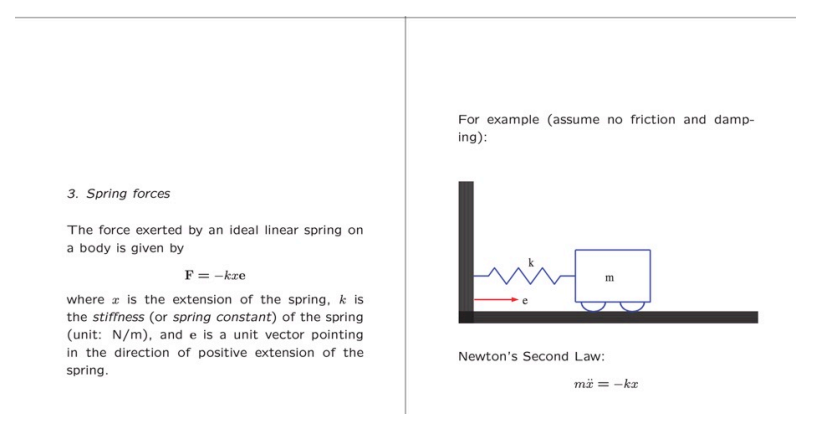
The generalized equations of translational and rotational motion that have been stated above for a system of particles are equally valid for the rigid body; shown below is a rigid body \(B\) in general 3D rotation (see Lecture 4 rigid body kinematics_ orientations.pdf for classification of types of motion).

The equations of motion this body are given as follows:

Translational:

\[\sum \mathbf{{F}}_i = m_B {}^{N}{\mathbf{{a}}}^{B^*} \]

Rotational:

\[\sum{\mathbf{{M}}}^{{{\mathbf{{F}}}_i}/{B^*}} + \sum \mathbf{{M}}_i = \frac{{}^N d} {\mathrm{d}t} {}^{N}{\mathbf{{H}}}^{B/{B^*}}\]

Let’s briefly examine the rotational equation further. Now, we know that:

\[{}^{N}{\mathbf{{H}}}^{B/{B^*}} = \left[I \right]^{B/B^*}\cdot {}^{N}{\boldsymbol{{\omega}}}^B\]

Now if the inertia scalars of \(B\) about \(B^*\) are defined in the \(B\) frame; for example:

\[{I_{xy}}^{B/B^*} \triangleq \int {\frac d{\mathrm{d}t}}(\mathbf{{p}}\times \hat{{\mathbf b}}_x) \cdot (\mathbf{{p}}\times \hat{{\mathbf b}}_y)\]

\[{I_{zz}}^{B/B^*} \triangleq \int {\frac d{\mathrm{d}t}}(\mathbf{{p}}\times \hat{{b}}_z) \cdot (\mathbf{{p}}\times \hat{{\mathbf b}}_z)\]

\[{}^N{\boldsymbol{{\omega}}}^B = \omega_x \hat{{\mathbf b}}_x + \omega_y \hat{{\mathbf b}}_y + \omega_z \hat{{\mathbf b}}_z\]

Then,

\[ \frac{{}^N d} {\mathrm{d}t} {}^{N}\mathbf{{H}}^{B/B^*} = {}^{B} {\frac d{\mathrm{d}t}} {}^{N}\mathbf{{H}}^{B/B^*} + {}^{N}\boldsymbol{{\omega}}^B \times {}^{N}\mathbf{{H}}^{B/B^*} \]

Or,

\[ \frac{{}^N d} {\mathrm{d}t} {}^{N}\mathbf{{H}}^{B/B^*} = \left[I\right]^{B/B^*} \cdot {}^{N}\boldsymbol{{\alpha}}^{B} + {}^{N}\boldsymbol{{\omega}}^B \times (\left[I\right]^{B/B^*} \cdot {}^{N}\boldsymbol{{\omega}}^B) \]

Where: \({}^{N}\boldsymbol{{\alpha}}^{B} = \alpha_x \hat{{\mathbf b}}_x + \alpha_y \hat{{\mathbf b}}_y + \alpha_z \hat{{\mathbf b}}_z\).

So, now we can look at what happens to the scalar equations of motion in each of the directions. We do so for two cases:

Case 1: No products of inertia

In this case, \(I_{xy}=I_{yz}=I_{zx}=0\). Therefore:

\[\begin{split} \frac{{}^N d} {\mathrm{d}t} {}^{N}\mathbf{{H}}^{B/B^*} = \begin{cases} \left[ I_x {\alpha}_x - (I_y - I_z) \omega_y \omega_z \right] \hat{\mathbf b}_x \\ \left[ I_y {\alpha}_y - (I_z - I_x) \omega_z \omega_x \right] \hat{\mathbf b}_y \\ \left[ I_z {\omega}_z - (I_x - I_y) \omega_x \omega_y \right] \hat{\mathbf b}_z \\ \end{cases} \end{split}\]

Case 2: No products of inertia and simple roatation.

In other words, \(I_{xy}=I_{yz}=I_{zx}=0\) and there is only one angula vecolity component.

Example 1: Simple pendulum

\[{}^{N}\boldsymbol{{\omega}}^{B} = \omega_z \hat{\mathbf b}_z \rightarrow {}^{N}\boldsymbol{{\alpha}}^{B} = \alpha_z \hat{\mathbf b}_z\]

So,

\[\frac{{}^N d} {\mathrm{d}t} {}^{N}\mathbf{{H}}^{B/B^*} = I_Z \alpha_z \hat{\mathbf b}_z\]

Then, we can derive the equations of motion.

Example 2: Pulley

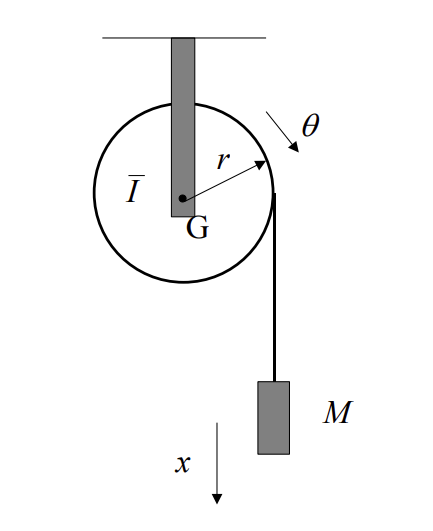
The system shown in the figure above consists of a pulley constrained to rotate about its centre of mass \(G\). A light cord is wrapped around the pulley and the free end is attached to a mass of \(10\;kg\). The radius of the pulley is \(0.15\;m\) and its moment of inertia about \(G\) is \(0.4\;kgm^2\).

If the mass is released from rest what will be its velocity after one revolution of the pulley.

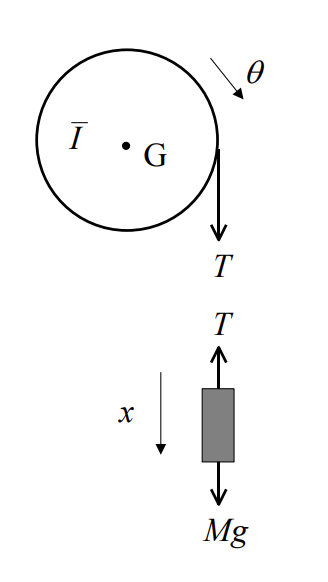
With reference to the free body diagram above, the pulley is constrained to rotate about its centre of mass, \(G\). Therefore the only equation of motion of importance is the balance of moments about the pulleys centre of mass as follows:

\[ \sum|\mathrm{\boldsymbol{M}_G}| = \bar{I}\alpha = \bar{I}\ddot{\theta} \]

Therefore,

\[ Tr=\bar{I}\ddot{\theta} \]

And for the mass, motion is in the x-direction only with no rotation.

\[ Mg-T=M\ddot{x} \]

Finally, from geometry,

\[ \theta = \frac{x}{r} \]

Therefore,

\[ \dot{\theta} = \frac{\dot{x}}{r} \]

And

\[ \ddot{\theta} = \frac{\ddot{x}}{r} \]

Hence we have three equations and three unknowns, \(T\), \(\ddot{x}\) and \(\ddot{\theta}\).

Eliminating \(T\) and \(\ddot{\theta}\) leaves:

\[ \ddot{x} = \frac{Mg}{\left(\frac{\bar{I}}{r^2} + M\right)} = \frac{10\times9.81}{\left(\frac{0.14}{0.15^2} + 10\right)} = 3.52 \;m/s^2 = \mathrm{constant} \]

After one revolution, the mass will have traveled a distance, \(s = 2\times S \times 0.15 = 0.942\;m\). For constant acceleration and zero initial velocity,

\[ \nu = \sqrt{2as} = \sqrt{2 \times 3.53 \times 0.942} = 2.58\;m/s \]