Time, Calendars and Launch Windows#

Prepared by: Hardit Saini, Emmanuel Airiofolo, Ilanthiraiyan Sivagnanamoorthy and Angadh Nanjangud

In this lecture we cover the following topics:

  1. Sidereal Time

  2. Calendars

  3. Launch Windows

Sidereal Time#

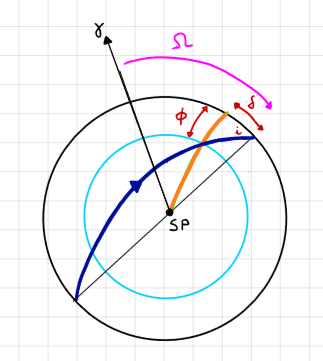
  • Local apparent sidereal time (Abbreviated LAST or LST): time measure based on the hour angle of \(\gamma\).

  • Sidereal day: the interval between two successive returns of \(\gamma\) to the same local meridian.

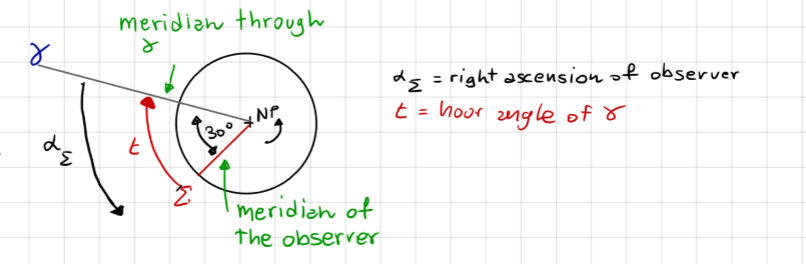
Figure 1

(213)#\[\text{LAST} = 30^\circ = \frac{30^\circ}{360^\circ} \times 24 \ \text{Hours} = 2 \ \text{Hours}\]

LAST coincides with the right ascension of the observer \(\alpha_\Sigma\), hence;

(214)#\[\text{LAST} = \alpha_\Sigma\]

Note: The sidereal time is measured with respect to a fixed direction, thus it is more useful for computing the time passage of spacecraft, whose orbits are defined with respect to the same fixed direction.

Solar Day vs Sidereal Day#

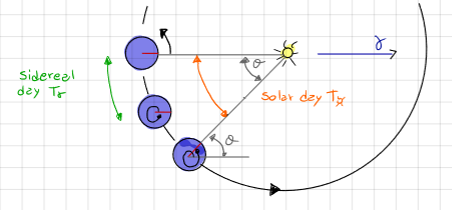
Figure 2

Sidereal Day \(T_\gamma = \frac{2 \pi}{\omega_e}\), with \(\omega_e\) the angular velocity of the Earth.

Solar Day \(T_{\circledcirc} = \frac{2 \pi + \theta}{\omega_e}\)

Note:

(215)#\[T_{\circledcirc} = \frac{2 \pi + \theta}{\omega_e} = T_\gamma + \frac{\theta}{\omega_e}\]

Hence, \(T_{\circledcirc} > T_\gamma\).

\(\theta\) is the angle swept by the Earth in one solar day, thus \(\theta = \frac{2 \pi}{Y}\) with \(Y\) the number of solar days in a year (\(Y = 365.256\) days).

(216)#\[T_{\circledcirc} = T_\gamma + \frac{2 \pi}{Y\omega_e} = T_\gamma + \frac{T_\gamma}{Y} = T_\gamma \left(1 + \frac{1}{Y}\right)\]

Hence:

(217)#\[Y T_{\circledcirc} = (Y + 1)T_\gamma\]

There are \(Y + 1\) sidereal days in 1 year.

\(T_{\circledcirc}\) = 24 hr \(\implies T_\gamma\) = 23 hr, 56 min, 4 sec.

Calendars#

Tropical year:#

Interval between two successive passages of the Sun to \(\delta\).

(218)#\[1 \ \text{tropical year} = 365.2422 \ \text{solar days} \ (\text{Laskar 1986})\]

or:

(219)#\[1 \ \text{tropical year} = 365.2422 \ \text{sidereal days}\]

Sidereal year:#

Interval between two successive passages of the Sun to a reference star.

Note: Due to the precession of the equinoxes, the tropical year is shorter than the sidereal year; \(\gamma\) moves clockwise.

Julian Calendar (46 BC)#

  • 12 months, regular year of 365 days, with a leap day added in February every 4 years.

    • It was estimated that a tropical year consisted of 365.25 solar days. To avoid a drift between the Julian calendar and the tropical year, 1 day was added every 4 years.

Gregorian Calendar (1582 AD)#

  • 12 months, regular year of 365 days, with a leap day added to February every 4 years except for secular years (e.g., 1700). The leap day is added to secular years that are multiples of 400 (e.g., 2000).

    • It was estimated that a tropical year consisted of 365.2425 days, thus the Julian year accumulates a 3-day difference every 4 centuries with respect to equinox time.

PROBLEM: Gregorian date yyyy/mm/dd hh:mm:ss is not practical for computations!

Julian Day#

  • Progressive number of days since noon, 1 January 4713 BC. For example:

\[2016/11/08 \quad 12:00:00 \quad \rightarrow \quad 2457692.0 \ \text{JD}\]

  • To work with smaller numbers, Modified Julian date is used:

(220)#\[\text{MJD} = \text{JD} - \text{ref}\]
\[\text{MJD} 2000 = \text{JD} - 2451545.5 \quad \text{(Now the reference is at midnight)}\]

Launch Windows#

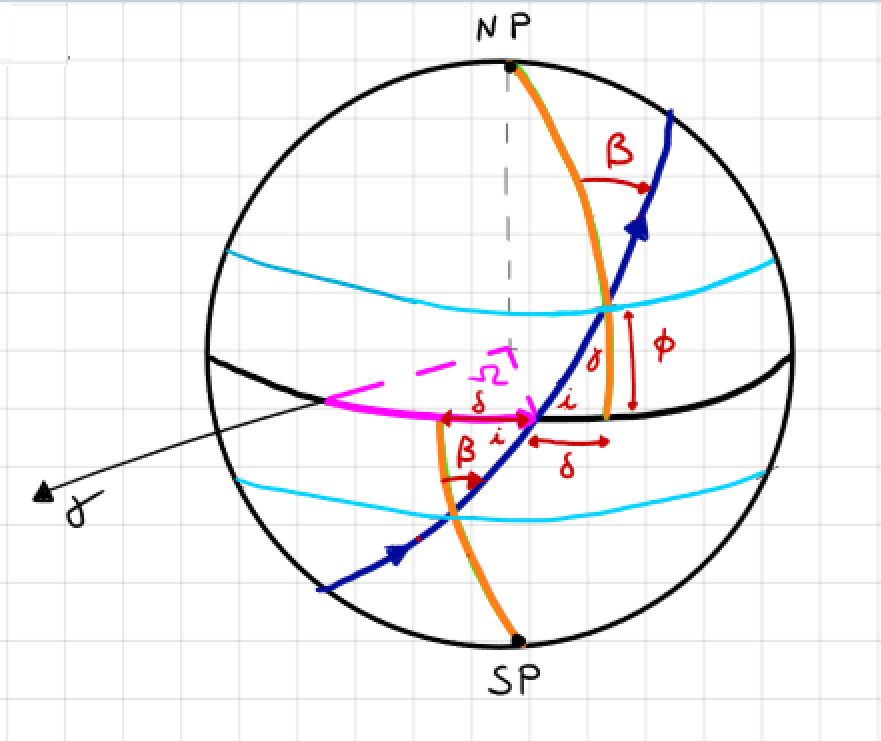
  • The launch window is the time when the launch site on the surface of the Earth passes through the orbital plane.

  • Determination of launch time (sidereal time) and launch direction.

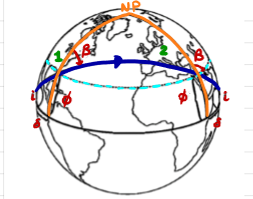
Figure 3

  • The launch site must pass through the orbit, thus three conditions:

    1. No launch window: \( \phi > i \quad \text{or} \quad \phi > 180^\circ - i \quad \text{(retrograde)} \)

    2. One launch window: \( \phi = i \quad \text{or} \quad \phi = 180^\circ - i \quad \text{(retrograde)} \)

    3. Two launch windows: \( \phi < i \quad \text{or} \quad \phi < 180^\circ - i \quad \text{(retrograde)} \)

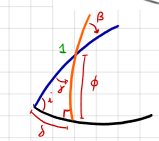
Figure 4

\( \text{NOTE: when } \phi = i, \text{ LAUNCH DUE EAST, we fully exploit the velocity of the launch site!} \)

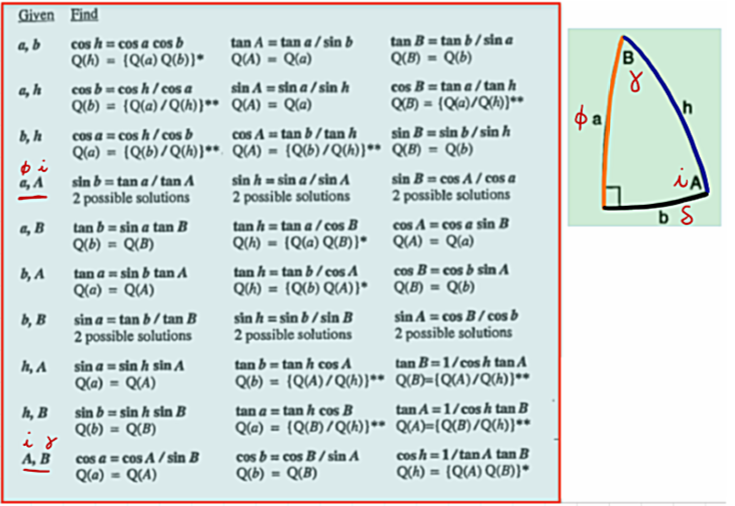
Given Data:

\(i\) is the orbit inclination.

\(\phi\) is the launch site latitude.

To be computed:

\(\delta\) is the window location angle.

\(\alpha\) is the direction auxiliary angle.

\(\beta\) is the launch azimuth: the angle from the north to the launch direction, positive clockwise.

\(\text{NOTE: launch sites have constraints on launch azimuth}\).

Right Spherical Triangle Formulae#

Figure 5

Launch Window: Prograde Orbit (i < \(90^\circ\)) and Northern Hemisphere#

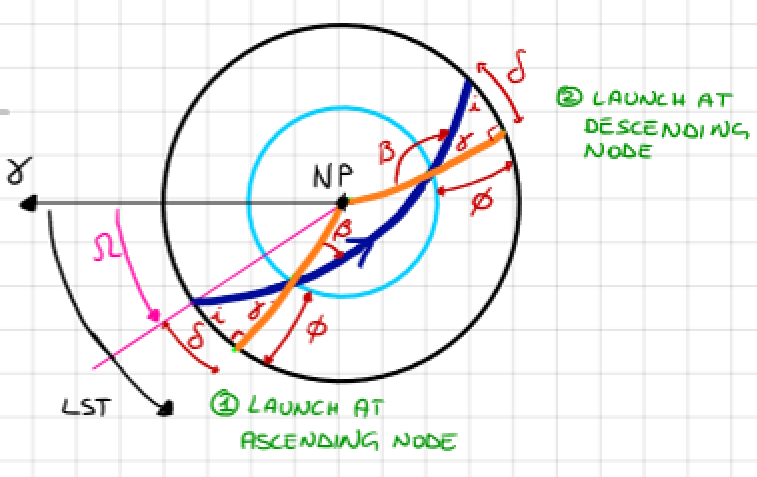
Figure 6

(221)#\[\sin \gamma = \frac{\cos i}{\cos \phi}\]
(222)#\[\sin \delta = \frac{\tan \phi}{\tan i} \quad \text{or} \quad (\cos \delta = \frac{\cos \gamma}{\sin i})\]

① Ascending Node:

(223)#\[\beta = \delta\]
(224)#\[\text{LST}_{\text{launch}} = \Omega + \delta\]

② Descending Node:

(225)#\[\beta = 180^\circ - \gamma\]
(226)#\[\text{LST}_{\text{launch}} = \Omega + 180^\circ - \delta\]

Note from (221):

(227)#\[\cos (i) = \sin \gamma \cos \phi \implies \boxed{\phi \leq i}\]
(228)#\[(\sin (\gamma) \geq 1 \implies \cos (i) \leq \cos (\phi))\]

A closer look at \(\boxed{\phi \leq i} \) suggests:

a. The latitude of launch site must be less than orbit inclination for a direct launch.

b. Equatorial orbit only from equatorial launch sites.

c. When \( \phi = i \), launch due East: optimal condition!

Launch Window: Retrograde Orbit \(( i \geq 90^\circ )\) and Northern Hemisphere#

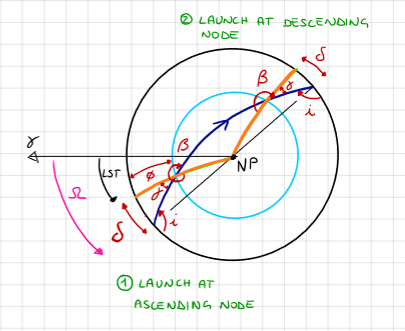
Figure 7

(229)#\[\sin \gamma = \frac{\cos (180^\circ - i)}{\cos \phi} = \frac{-\cos i}{ \cos \phi}\]
(230)#\[\sin \delta = \frac{\tan \phi}{\tan (180^\circ - i)} = \frac{-\tan \phi}{\tan i}\]

① Ascending Node:

(231)#\[\beta = 360^\circ - \gamma\]
(232)#\[\text{LST}_{\text{launch}} = \Omega - \delta\]

② Descending Node:

(233)#\[\beta = 180^\circ + \delta\]
(234)#\[\text{LST}_{\text{launch}} = \Omega + 180^\circ + \delta\]

Launch Window: From Southern Hemisphere#

Figure 8

  • The launch azimuth is the same as the northern hemisphere.

  • \(\text{LST}_{\text{launch}}\) is different.

Example: Ascending Node:

Figure 9

(235)#\[\text{LST}_{\text{launch}}^{\text{North}} = \Omega + \delta\]
(236)#\[\text{LST}_{\text{launch}}^{\text{South}} = \Omega - \delta\]