Problem Set 1

Problem Set 1#

Question 1#

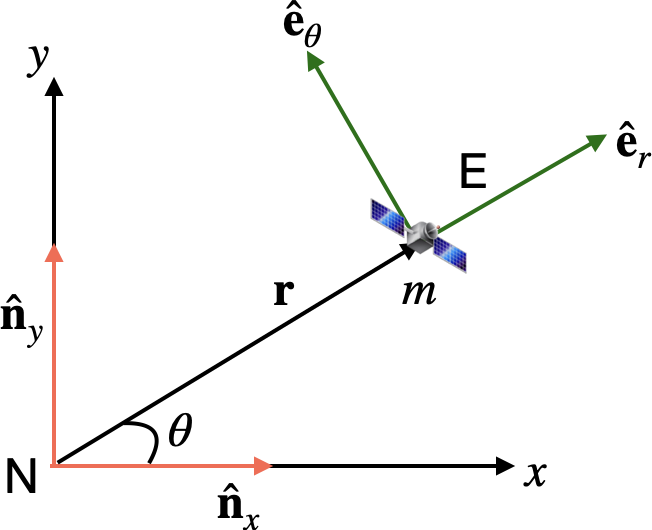
In the figure above, N is an inertial frame comprising right-handed unit vectors \({\bf \hat n}_x\) and \({\bf\hat n}_y\). E is reference frame attached to the satellite comprising \({\bf \hat e}_r\) and \({\bf \hat e}_\theta\); note that \({\bf e}_r\) is directed along \(\bf r\) and \({\bf e}_\theta\) is orthogonal to \({\bf e}_r\). What is the relationship between \({\bf e}_r\) and \({\bf e}_\theta\) and the unit vectors \({\bf \hat n}_x\) and \({\bf\hat n}_y\)? By differentiating these expressions with respect to time, show that:

\(\dot {\bf e}_r = \dot\theta {\bf e}_\theta\)

and

\(\dot {\bf e}_\theta = -\dot\theta {\bf e}_r\)

Your written answers go here (and create more markdown cells if you wish to)#

# Your coded answers here (and create more Code cells if you wish to)

Question 2#

The position of a satellite is given by \({\bf r} = r {\bf e}_r\). It’s velocity is given by \({\bf v} = \dot {\bf r}\). Using the results from question 1, show that:

\({\bf v} = \dot r {\bf e}_r + r \dot\theta {\bf e}_\theta\).

The angular momentum per unit mass is given by: \({\bf h} = {\bf r} \times {\bf v}\). Find an expression for the angular momentum of the satellite. Which direction does it point?

Your written answers go here (and create more markdown cells if you wish to)#

# Your coded answers here (and create more Code cells if you wish to)

Question 3#

The velocity of a satellite in orbit is given by \({\bf v} = \dot {\bf r}\). Using the results of Question 1, show that the acceleration is:

\((\ddot r - r \dot\theta^2) {\bf e}_r + \frac{1}{r} \frac{d}{dt}(r^2 \dot\theta) {\bf e}_\theta\)

Your written answers go here (and create more markdown cells if you wish to)#

# Your coded answers here (and create more Code cells if you wish to)

Question 4#

The gravitational force acting on an orbiting satellite is given by:

\({\bf F} = -\frac{\mu m}{r^3}{\bf r}\)

where \(\mu\) is the gravitational parameter and and \(m\) is the mass of the satellite. Write down the vector equation of motion and then write down its radial (direction \({\bf e}_r\) ) and azimuthal (direction \({\bf e}_\theta\)) components.