Orbital Elements (Part 2)#
Prepared by: Noah Leigh, Ilanthiraiyan Sivagnanamoorthy, and Angadh Nanjangud
In this lecture we aim to cover the following topics:
Orbital Elements from Position and Velocity Vectors#
Orbital Parameters
Calculate the semi-major axis \(a\) from the Vis-Viva equation, given by Equation (89):
\[\frac{1}{2}v^2 - \frac{\mu}{r}= -\frac{\mu}{2a}\]
Compute the eccentricity \(e\) (see Equation (75)):
\[\mathbf{e} = \frac{\mathbf{v} \times \mathbf{h}}{\mu} - \frac{\mathbf{r}}{|\mathbf{r}|}\]
Compute the inclination \(i\) from:
(148)#\[h_z=h \cos i\]
Compute the line of nodes from \({\mathbf{n}} = \hat{\mathbf k} \times {\mathbf h}\) and then the right ascension of the ascending node \(\Omega\) from:
(149)#\[n_x = n \cos \Omega\]where \(n_x\) is the x-component of \(\mathbf{n}\) and \(n\) is the magnitude of \(\mathbf{n}\). The following logic determines the correct quadrant for \(\Omega\):
If \(n_y \geq 0\), then \(\Omega = \cos^{-1} \left( \frac{n_x}{n} \right)\). In this case, \(\Omega \in [0, 180^\circ]\)
If \(n_y < 0\), then \(\Omega = 360^\circ - \cos^{-1} \left( \frac{n_x}{n} \right)\). In this case, \(\Omega \in (180^\circ, 360^\circ)\)
Compute the argument of perigee \(\omega\) from:
(150)#\[\cos \left(\omega\right) = \frac{\mathbf{n} \cdot \mathbf{e}}{|\mathbf{n}| |\mathbf{e}|}\]To determine the correct quadrant for \(\omega\), one examines the sign of \(e_z\), the z-component of the eccentricity vector \(\mathbf{e}\):
If \(e_z \geq 0\), then \(\omega = \cos^{-1}\left(\frac{\mathbf{n} \cdot \mathbf{e}}{ne}\right)\). In this case, \(\omega \in [0, 180^\circ]\).
If \(e_z < 0\), then \(\omega = 360^\circ - \cos^{-1}\left(\frac{\mathbf{n} \cdot \mathbf{e}}{ne}\right)\). In this case, \(\omega \in (180^\circ, 360^\circ)\).
Compute the true anomaly \(\theta\) from:
(151)#\[\mathbf{r}\cdot\mathbf{e} = |\mathbf{r}||\mathbf{e}|\cos \left( \theta \right)\]To determine the correct quadrant for \(\theta\), one needs to calculate \(v_r = \mathbf{v}\cdot\hat{\mathbf{r}}\):
If \(v_r \geq 0, \theta = \cos^{-1}\left(\frac{\mathbf{r}\cdot\mathbf{e}}{|\mathbf{r}||\mathbf{e}|}\right)\). In this case, \(\theta \in [0, 180^\circ]\).
If \(v_r < 0, \theta = 360^\circ - \cos^{-1}\left(\frac{\mathbf{r} \cdot \mathbf{e}} {|\mathbf{e}||\mathbf{r}|}\right)\). In this case, \(\theta \in (180^\circ, 360^\circ)\).
Note
Orbital parameters can be singular in certain conditions!
Rotation Matrix (Direction Cosines Matrix)#
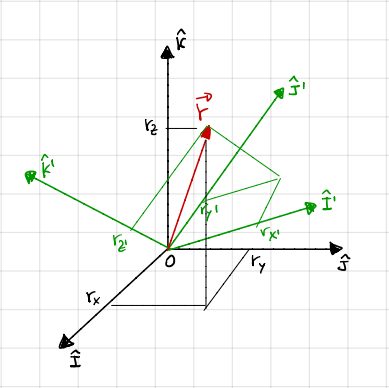
Fig. 19 Shows the two different reference frames, before transformation in black and after in green.#
Let’s define the unit vectors of two frames:
In the original frame: \(\left(\mathbf{ \hat{I}, \hat{J}, \hat{K} }\right)\)
In the transformed frame: \(\left( \mathbf{\hat{I}', \hat{J}', \hat{K}'} \right)\)
We want to express a vector r in two frames:
In the original frame: \(\mathbf{r} = (\mathbf{r_x, r_y, r_z})\)
In the transformed frame: \(\mathbf{r'} = \left(\mathbf{r'_x, r'_y, r'_z}\right)\)
Matrix Transformation:#
The transformation from the original frame to the new frame can be written as:
Each row of A contains the components of \(\mathbf{I',J',K'}\) in the \(\mathbf{I,J,K}\) reference frame. and vice versa for the columns.
Properties of the Rotation Matrix, \(A\):#
The columns of \(A\) contain the components of the unit vectors \(\mathbf{I, J, K}\) in the transformed frame \(\mathbf{I', J', K'}\).
The inverse transformation is given by:
Since \(A\) is an orthogonal matrix, the inverse of \(A\) is equal to its transpose:
This gives us the property:
Where \(I\) is the identity matrix.
The norm of each row of \(A = 1\) and the dot product between rows = 0 \(\Rightarrow\) 6 constraints \(\Rightarrow\) 9 elements - 6 constraints = 3 Degrees of Freedom.
Successive Rotations:#
If two successive rotations are performed, say \(A_1\) and \(A_2\), the net transformation matrix \(A\) is the product of the two:
This allows us to deal with complex rotations as a series of simpler rotations.
Rotation About a Single Axis:#
For rotation about the \(\mathbf{I}\) \(\left(\mathbf{\hat{I}}\equiv\mathbf{\hat{I}'}\right)\):
\(\mathbf{r'} = A_x(\alpha)\mathbf{r}\)
Inverse - \(\mathbf{r}=A_x(\alpha)^T\mathbf{r'}=A_x(-\alpha)\mathbf{r'}\)
We can also associate an angular velocity to this rotation \(\boldsymbol{\omega}=\dot{\alpha}\mathbf{\hat{I}}\).
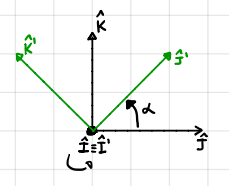
Fig. 20 Shows a rotation about x-axis, before transformation in black and after in green.#
For rotation about the \(\mathbf{J}\) \(\left(\mathbf{\hat{J}}\equiv\mathbf{\hat{J}'}\right)\):
\(\mathbf{r'} = A_y(\alpha)\mathbf{r}\)
Inverse - \(\mathbf{r}=A_y(\alpha)^T\mathbf{r'}=A_y(-\alpha)\mathbf{r'}\)
We can also associate an angular velocity to this rotation \(\boldsymbol{\omega}=\dot{\alpha}\mathbf{\hat{J}}\).
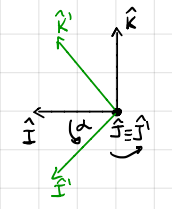
Fig. 21 Shows a rotation about y-axis, before transformation in black and after in green.#
For rotation about the \(\mathbf{K}\) \(\left(\mathbf{\hat{K}}\equiv\mathbf{\hat{K}'}\right)\):
\(\mathbf{r'} = A_z(\alpha)\mathbf{r}\)
Inverse - \(\mathbf{r}=A_z(\alpha)^T\mathbf{r'}=A_z(-\alpha)\mathbf{r'}\)
We can also associate an angular velocity to this rotation \(\boldsymbol{\omega}=\dot{\alpha}\mathbf{\hat{K}}\).
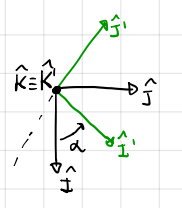
Fig. 22 Shows a rotation about z-axis, before transformation in black and after in green.#
ECI to Perifocal Frame#
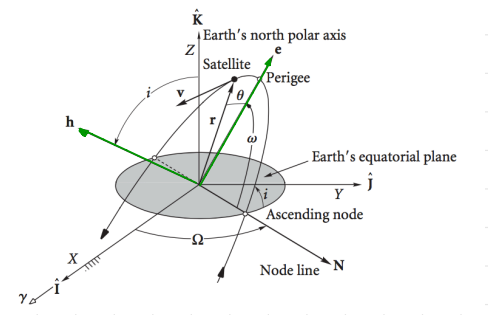
Fig. 23 Shows a satellite’s orbit described relative to Earth.#
Composition of Rotations:#
To rotate from the ECI (Earth-Centered Inertial) frame to the perifocal frame, we use three successive rotations:
Rotation by \(\Omega\) about the z-axis:
\[ A_z(\Omega) \]Rotation by \(i\) about the x-axis:
\[ A_x(i) \]Rotation by \(\omega\) about the z-axis:
\[ A_z(\omega) \]
The total transformation matrix, using successive rotations (152), is:
with the respective direction matrices.
Transformation:
Passage from the ECI frame to the perifocal frame is given by the composition of three rotations:
(153)#\[\mathbf{r}_{perifocal} = A_z(\omega) A_x(i) A_z(\Omega) \mathbf{r}_{ECI}\]
Inverse Transformation:
To transform from the perifocal frame back to ECI:
\[ \mathbf{r}_{ECI}=\left[A_z(\omega)A_x(i)A_z(\Omega)\right]^T\mathbf{r}_{perifocal} =A^T_z(\Omega)A^T_x(i)A^T_z(\omega)\mathbf{r}_{perifocal} \](154)#\[\mathbf{r}_{ECI} = A_z(-\Omega) A_x(-i) A_z(-\omega) \mathbf{r}_{perifocal}\]
Ephemeris#
Ephemeris are the position and velocity vectors as a function of time. They are typically provided as: \(t_0, a, e, i, \Omega, \omega, M_0\).
Note that, except for \(t\) and \(M_0\), all the other parameters are constant.
Problem: We wish to compute \(\mathbf{r}\) and \(\mathbf{v}\) at a general time, \(t\), in ECI frame.
Solution:
First, we compute \(n = \sqrt\frac{\mu}{a^3}\).
Then we calculate the current mean anomaly \(M = n(t - t_0) + M_0\).
Solve Kepler’s equation, given by \(M = E - e\sin(E)\), for \(E\) (the eccentric anomaly).
Find the true anomaly \(\theta\) from:
(155)#\[\tan \left(\frac{E}{2}\right) = \sqrt{\frac{1+e}{1-e}} \tan\left( \frac{\theta}{2} \right)\]Find \(h\) from \(h = \sqrt{p \mu} = \sqrt{a(1-e^2)\mu}\).
Compute the position vector in the perifocal frame:
(156)#\[\mathbf{r}_{perifocal} = \frac{\frac{h^2}{\mu}}{1 + e \cos \theta } \bigr( \cos \theta \mathbf{\hat{p}} + \sin \theta \mathbf{\hat{q}} \bigr)\]
Compute the velocity vector in the perifocal frame:
(157)#\[\mathbf{v}_{perifocal} = \frac{\mu}{h} \bigr( -\sin \theta \mathbf{\hat{p}} + (e + \cos \theta) \mathbf{\hat{q}} \bigr)\]


