Vectors (Brief Recap)

Prepared by: Hardit Saini, Emmanuel Airiofolo and Angadh Nanjangud

In this lecture we cover the following topics:

1. Vector Operations

2. Vector Operations: Cross Product and Related Formulas

3. Time Derivative of a Vector

4. References

• A vector is a quantity with a direction and a magnitude.

• \(\vec{\rm{r}}\), \(\underline{\rm{r}}\), \(\bf{r}\) are all possible notations for vector quantities.

• We describe a vector by its components:
  \(\vec{\rm{r}}\) = \(\rm{r_x} \hat{\bf{i}}\) + \(\rm{r_y} \hat{\bf{j}}\) + \(\rm{r_z} \hat{\bf{k}}\) = (\(\rm{r_x}, \rm{r_y}, \rm{r_z}\))

  where \(\hat{\bf{i}}\), \(\hat{\bf{j}}\), and \(\hat{\bf{k}}\) are unit vectors aligned with a triad of orthogonal axes.

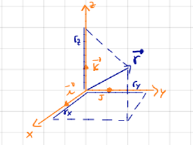
• The magnitude is indicated by \(\|\bf{r}\|\) or simply by \(r\), and

(1)\[r = \sqrt{r_x^2 + r_y^2 + r_z^2}\]

Vector Operations

Multiplication of a Scalar with a Vector

• When a vector \(\bf{A}\) is multiplied by a scalar \(\rm{Q}\), the result is a new vector \(\rm{Q}\bf{A}\), which has the same direction as \(\bf{A}\) but a magnitude that is \(|\rm{Q}|\) times the magnitude of \(\bf{A}\).

(2)\[\rm{Q} {\bf{A}} = \rm{Q} (A_x \hat{\bf{i}} + A_y \hat{\bf{j}} + A_z \hat{\bf{k}}) = (\rm{Q} A_x) \hat{\bf{i}} + (\rm{Q} A_y) \hat{\bf{j}} + (\rm{Q} A_z) \hat{\bf{k}}\]

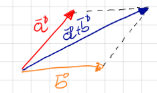
• The sum of vectors \(\bf{A}\) and \(\bf{B}\) is a vector \(\bf{C}\) such that:

(3)\[\bf{C} = \bf{A} + \bf{B} = (\rm{A_x} + \rm{B_x}) \hat{\bf{i}} + (\rm{A_y} + \rm{B_y}) \hat{\bf{j}} + (\rm{A_z} + \rm{B_z}) \hat{\bf{k}}\]

• Parallelogram Rule: The sum of two vectors can also be represented geometrically using the parallelogram rule: Place the vectors \(\bf{A}\) and \(\bf{B}\) tail to tail. Draw a parallelogram where \(\bf{A}\) and \(\bf{B}\) are adjacent sides. The interception of the two projected lines represents the point where \(\bf{A}\) is summed with \(\bf{B}\), \(\bf{A} + \bf{B}\).

Dot Product Rule

• The dot product (or scalar product) of two vectors \(\bf{A}\) and \(\bf{B}\) is defined as:

(4)\[{\bf{A}} \cdot {\bf{B}} = A_x B_x + A_y B_y + A_z B_z\]

(5)\[{\bf{A}} \cdot {\bf{B}} = {|\bf{A}|} {|\bf{B}|} \cos(\theta)\]

• Where \(\theta\) is the angle between \(\bf{A}\) and \(\bf{B}\).

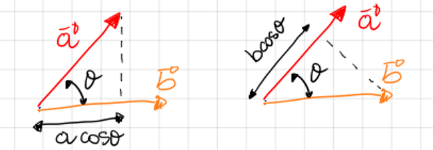
If one of the vectors is a unit vector (say, \(\hat{\bf{B}}\)), the dot product gives the projection of \(\bf{A}\) onto \(\hat{\bf{B}}\):

(6)\[{\bf{A}} \cdot {\bf{\hat{B}}} = {|\bf{A}|} \cos(\theta)\]

• This is because \(|\hat{\bf{B}}|\) = 1.

Vector Operations: Cross Product and Related Formulas

Cross Product

• The cross product of two vectors \(\bf{A}\) and \(\bf{B}\), denoted \(\bf{A} \times \bf{B}\), results in a vector \(\bf{C}\) that is perpendicular to both \(\bf{A}\) and \(\bf{B}\).

• The magnitude of \(\bf{A} \times \bf{B}\) is given by:

(7)\[|\bf{A} \times \bf{B}| = |\bf{A}| |\bf{B}| \sin(\theta)\]

Where \(\theta\) is the angle between \(\bf{A}\) and \(\bf{B}\).

• The direction of \(\bf{A} \times \bf{B}\) is determined by the right-hand rule.

(Cross, 2024)

(8)\[\begin{split}{\bf{A}} \times {\bf{B}} = \begin{vmatrix} \hat{\bf{i}} & \hat{\bf{j}} & \hat{\bf{k}} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{vmatrix} = \left( A_y B_z - A_z B_y \right) \hat{\bf{i}} - \left( A_x B_z - A_z B_x \right) \hat{\bf{j}} + \left( A_x B_y - A_y B_x \right) \hat{\bf{k}}\end{split}\]

Properties of the Cross Product

• Anticommutative Property:

(9)\[{\bf{A}} \times {\bf{B}} = - ({\bf{B}} \times {\bf{A}})\]

• Distributive Property:

(10)\[{\bf{A}} \times ({\bf{B}} + {\bf{C}}) = {\bf{A}} \times {\bf{B}} + {\bf{A}} \times {\bf{C}}\]

• Scalar Multiplication:

(11)\[(k {\bf{A}}) \times {\bf{B}} = k ({\bf{A}} \times {\bf{B}}) = {\bf{A}} \times (k {\bf{B}})\]

• Triple Vector Product involves three vectors \(\bf{A}\), \(\bf{B}\), and \(\bf{C}\):

(12)\[{\bf{A}} \times ({\bf{B}} \times {\bf{C}}) = ({\bf{A}} \cdot {\bf{C}}) {\bf{B}} - ({\bf{A}} \cdot {\bf{B}}) {\bf{C}}\]

or

(13)\[({\bf{A}} \times {\bf{B}}) \times {\bf{C}} = ({\bf{C}} \cdot {\bf{B}}) {\bf{A}} - ({\bf{C}} \cdot {\bf{A}}) {\bf{B}}\]

• The Scalar Triple Product of three vectors \(\bf{A}\), \(\bf{B}\), and \(\bf{C}\) is a scalar quantity:

(14)\[{\bf{A}} \cdot ({\bf{B}} \times {\bf{C}})\]

This scalar represents the volume of the parallelepiped formed by the vectors \(\bf{A}\), \(\bf{B}\), and \(\bf{C}\).

Admin (2019)

• It can be computed as:

(15)\[\begin{split}{\bf{A}} \cdot ({\bf{B}} \times {\bf{C}}) = \begin{vmatrix} A_x & A_y & A_z \\ B_x & B_y & B_z \\ C_x & C_y & C_z \end{vmatrix}\end{split}\]

Interesting to note:

(16)\[{\bf{A}} \cdot ({\bf{B}} \times {\bf{C}}) = {\bf{B}} \cdot ({\bf{C}} \times {\bf{A}}) = {\bf{C}} \cdot ({\bf{A}} \times {\bf{B}})\]

Time Derivative of a Vector

• The time derivative of a vector \(\bf{A}\) represents how the vector changes with respect to time.

In an Inertial Reference Frame

• The time derivative of a vector \(\bf{r}\) in an inertial reference frame is given by:

(17)\[\frac{d{\bf{r}}}{dt} = \frac{d}{dt}(x) {\hat{\bf{i}}} + \frac{d}{dt}(y) {\hat{\bf{j}}} + \frac{d}{dt}(z) {\hat{\bf{k}}}\]

In a Rotating Reference Frame with angular velocity \(\boldsymbol{\omega}\), the time derivative of the vector \(\bf{r}\) must account for the rotation:

(18)\[\left( \frac{d{\bf{r}}}{dt} \right)_{\text{inertial}} = \left( \frac{d{\bf{r}}}{dt} \right)_{\text{rotating}} + (\boldsymbol{\omega} \times {\bf{r}})\]

where:

\(\left( \frac{d{\bf{r}}}{dt} \right)_{\text{rotating}}\) is the time derivative in the rotating frame.

\(\left( \frac{d{\bf{r}}}{dt} \right)_{\text{inertial}}\) is the time derivative in the inertial frame.

\(\boldsymbol{\omega}\) is the angular velocity of the rotating frame.

\(\times\) denotes the cross product (see above for more information).

This can also be expressed as:

(19)\[\left( \frac{d{\bf{r}}}{dt} \right)_{\text{rotating}} = \left( \frac{d{\bf{r}}}{dt} \right)_{\text{inertial}} - (\boldsymbol{\omega} \times {\bf{r}})\]

References

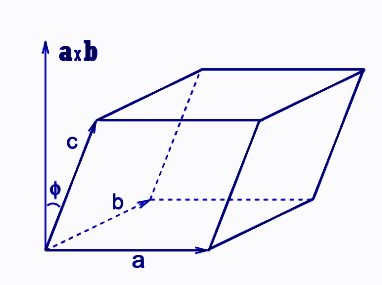
Admin (2019). Parallelepiped- Definition, Volume and Area Formula, Example. [online] BYJUS. Available at: https://byjus.com/maths/parallelepiped/ [Accessed 2 Sep. 2024].

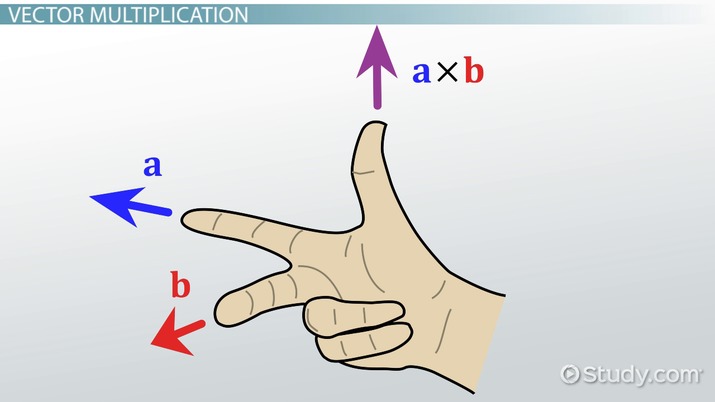
Cross (2024). Cross Product & Right Hand Rule | Formula, Applications & Example - Video | Study.com. [online] study.com. Available at: https://study.com/academy/lesson/video/cross-product-right-hand-rule-definition-formula-examples.html [Accessed 2 Sep. 2024].